Think Julia

Comme d'habitude, il convient au moins d'essayer de résoudre les exercices avant d'en lire les solutions.

13-1-1. Exercice 13-1▲

13-1-2. Exercice 13-2▲

13-1-3. Exercice 13-3▲

13-1-4. Exercice 13-4▲

Avec les mêmes données en entrée, la plupart des programmes informatiques produisent les mêmes données en sortie à chaque exécution. Ces programmes sont dits déterministes. Le déterminisme est généralement souhaité, puisque nous souhaitons que le même calcul donne le même résultat. Cependant, dans certaines applications (comme la sécurité informatique, l'analyse mathématique, les jeux, etc.), nous tenons à ce que l'ordinateur produise des données aléatoires.

Rendre un programme véritablement non déterministe (c'est-à-dire stochastique) est une tâche difficile. Néanmoins, il existe des moyens de le rendre au moins quasi non déterministe. Un de ces moyens consiste à utiliser des algorithmes qui fournissent des nombres pseudoaléatoires. Ces nombres ne sont pas vraiment aléatoires, parce qu'ils sont produits par un calcul déterministe, mais, en première analyse, il est pratiquement impossible de les distinguer de nombres réellement sortis au hasard.

La fonction rand retourne un flottant aléatoire entre 0.0 et 1.0 (y compris 0.0, mais pas 1.0). Chaque fois que rand est appelée, un nombre extrait d'une longue série est produit. Par exemple, nous pouvons faire tourner cette boucle :

for i in 1:10
    x = rand()
    println(x)
end

La fonction rand est susceptible de prendre un itérateur ou un tableau comme argument et elle retourne un élément aléatoire :

for i in 1:10 
    x = rand(1:6) 
    print(x, " ") 
end

13-2-1. Exercice 13-5▲

julia> t = ['a', 'a', 'b'];

julia> histogram(t)
Dict{Any,Any} with 2 entries:
'a' => 2
'b' => 1

Dans un premier temps, essayez les exercices précédents avant de poursuivre. Dans un second temps, rendez-vous sur cette page où vous pouvez télécharger le texte brut UTF-8 de l'œuvre de Victor Hugo intitulée « Notre-Dame de Paris ». Une fois le fichier enregistré sous notre_dame_de_paris.txt, supprimez l'en-tête jusqu'au titre « LIVRE PREMIER » non inclus.

À présent, voici un programme qui lit un fichier et construit un histogramme des mots inclus dans ce fichier :

function processfile(filename) 
    hist = Dict()
    for line in eachline(filename)
        processline(line, hist)
    end
    hist
end;

function processline(line, hist)
    line = replace(line, '-' =>  ' ')
    for word in split(line)
        word = string(filter(isletter, [word...])...)
        word = lowercase(word)
        hist[word] = get!(hist, word, 0) + 1 
    end 
end;

hist = processfile("/home/chemin_vers_fichier/notre_dame_de_paris.txt");

Ce programme lit le fichier notre_dame_de_paris.txt.

processfile parcourt en boucle les lignes du fichier, les passant une à une à processline. L'histogramme hist est utilisé comme un accumulateur.

processline utilise la fonction replace pour remplacer les traits d'union par des espaces avant d'utiliser split pour diviser la ligne traitée en un tableau de chaînes de caractères. La boucle for de processline traverse le tableau de mots et utilise filter, islettre et lowercase pour supprimer la ponctuation et convertir les caractères en minuscules.(32)

Enfin, processline met à jour l'histogramme soit en créant un nouvel élément en cas de première détection, soit en incrémentant un élément existant.

Pour compter le nombre total de mots dans le fichier, il faut additionner les fréquences dans l'histogramme :

function totalwords(hist)
    sum(values(hist)) 
end

Le nombre de mots différents n'est que le nombre d'éléments dans le dictionnaire :

function differentwords(hist) 
    length(hist)
end

Voici le code permettant d'afficher les résultats :

julia> println("Nombre total de mots: ", totalwords(hist)) 
Nombre total de mots: 172053

julia> println("Nombre de mots différents: ", differentwords(hist)) 
Nombre de mots différents: 17510

Pour trouver les mots les plus courants, nous pouvons (i) créer un tableau de tuples où chacun d'eux contient un mot et sa fréquence d'apparition et (ii) le trier. La fonction suivante prend un histogramme et retourne un tableau de tuples d'occurrence des mots :

function mostcommon(hist)
    t = []
    for (key, value) in hist
        push!(t, (value, key)) 
    end
    reverse(sort(t))
end

Dans chaque tuple, la fréquence apparaît en premier, de sorte que le tableau résultant est trié par fréquences. Voici une boucle qui affiche les 10 mots les plus courants :

t = mostcommon(hist) 
println("Les mots les plus courants sont:") 
for (freq, word) in t[1:10]
    println(word, "\t", freq)
end

Plutôt qu'un espace, un caractère de tabulation (\t) est employé comme séparateur. De cette manière, la deuxième colonne est alignée. Voici les résultats pour Notre-Dame de Paris :

Les mots les plus courants sont:
  de       8263
  la       5427
  et       4585
  le       4124
  à        3363
  les      2456
  il       2446
  un       2042
  que      2033
  qui      1978

Nous avons vu des fonctions internes à Julia qui prennent des arguments optionnels (voir l'exercice 8.15.1Exercice 8-7). Il est également possible d'écrire des fonctions définies par le programmeur avec des arguments optionnels. Par exemple, voici une fonction qui affiche les mots les plus courants dans un histogramme :

function printmostcommon(hist, num=10)
    t = mostcommon(hist)
    println("Les mots les plus courants sont: ")
    for (freq, word) in t[1:num] 
        println(word, "\t", freq) 
    end 
end

Le premier paramètre est obligatoire, le second facultatif. La valeur par défaut de num est 10.

Si un seul argument est fourni :

printmostcommon(hist)

num prend la valeur par défaut. Si vous fournissez deux arguments :

printmostcommon(hist, 20)

num prend la valeur de l'argument indiqué. En d'autres termes, l'argument optionnel remplace la valeur par défaut.

Si une fonction possède à la fois des paramètres obligatoires et facultatifs, tous les paramètres obligatoires apparaîtront les premiers.

Trouver les mots d'un livre, qui ne sont pas dans la liste de mots de mots_FR.txt revient à un problème de soustraction d'ensembles, c'est-à-dire trouver « les mots du livre moins les mots de la liste ».

subtract prend les dictionnaires d1 et d2 et, ensuite, retourne un nouveau dictionnaire qui contient toutes les clés de d1 qui ne se trouvent pas dans d2. Comme nous ne nous soucions pas vraiment des valeurs, nous pouvons toutes les fixer à nothing.

function subtract(d1, d2)
    res = Dict() 
    for key in keys(d1)
        if key ∉ keys(d2)
            res[key] = nothing
        end
    end 
    res
end

En vue de trouver les mots de Notre-Dame de Paris n'appartenant pas au fichier mots_FR.txt, nous pouvons utiliser processfile pour construire un histogramme associé à mots_FR.txt, et ensuite subtract :

words = processfile("mots_FR.txt") 
diff = subtract(hist, words)
println("Mots du roman n'appartenant pas à la liste mots_FR.txt:")
for word in keys(diff)
    print(word, " ")
end

Voici un bref extrait des résultats obtenus dans le cas de Notre-Dame de Paris :

Mots du roman n'appartenant pas à la liste mots_FR.txt: 
lambrissé pâtisserie polyèdre magnétisme apostrophé damoiselles caballero gisante bretonne…

Certains de ces mots sont des noms, des adverbes, etc. D'autres, comme « damoiselles », ne sont plus d'usage courant en français. Toutefois, certains sont des mots courants qui devraient absolument figurer dans la liste.

13-6-1. Exercice 13-6▲

Pour choisir un mot aléatoire dans l'histogramme, l'algorithme le plus simple consiste à construire un tableau contenant plusieurs copies de chaque mot selon la fréquence observée. Ensuite, il faut les extraire du tableau :

function randomword(h)
    t = []
    for (word, freq) in h
        for i in 1:freq
            push!(t, word)
        end 
    end
    rand(t)
end

Une autre possibilité consiste à :

1. Utiliser des clés pour obtenir un tableau des mots du livre ;
2. Construire un tableau qui contient la somme des occurrences d'un mot (voir l'exercice 10.15.2Exercice 10-2). Le dernier élément de ce tableau est le nombre total (n) de mots dans le livre ;
3. Choisir un nombre aléatoire compris entre 1 et n. Utiliser une recherche par bissection (voir exercice 10.15.10Exercice 10-10) pour trouver l'indice où le nombre aléatoire pourrait être inséré dans la somme ;
4. Utiliser l'indice pour trouver le mot correspondant dans le tableau de mots.

13-7-1. Exercice 13-7▲

Si quelqu'un choisissait au hasard des mots du roman Notre-Dame de Paris, il pourrait se faire une idée du vocabulaire, mais il n'obtiendrait très probablement pas une phrase cohérente. Voici le résultat d'une extraction aléatoire :

supplie des jours société de elle me vie en je

Une série de mots pris au hasard présente rarement du sens, car il n'existe pas de relation entre les mots successifs. Par exemple, dans une phrase sémantiquement correcte, on attend qu'un article comme « le » soit très probablement suivi d'un adjectif ou d'un nom, mais pas d'un verbe et encore moins d'un adverbe.

L'analyse de Markov est une manière d'établir ce genre de relations. Pour une séquence de mots donnée, cette analyse caractérise la probabilité qu'un mot en suive un autre. Par exemple, voici un extrait du poème Liberté de Paul Éluard :

Sur mes cahiers d’écolier
Sur mon pupitre et les arbres
Sur le sable sur la neige
J’écris ton nom
[…]
Sur la lampe qui s’allume
Sur la lampe qui s’éteint
Sur mes maisons réunies
J’écris ton nom
[…]
Sur mes refuges détruits
Sur mes phares écroulés
Sur les murs de mon ennui
J’écris ton nom
[…]
Et par le pouvoir d’un mot
Je recommence ma vie
Je suis né pour te connaître
Pour te nommer

Liberté

En l'occurrence, l'expression « la lampe » est toujours suivie du pronom relatif « qui », alors que l'expression « lampe qui » peut être suivie des verbes pronominaux conjugués au présent de l'indicatif « s'allume » ou « s'éteint ».

L'analyse de Markov consiste en une mise en correspondance de chaque préfixe (comme « la lampe » ou « lampe qui ») avec tous les suffixes possibles (comme « s'allume » ou « s'éteint »).

Grâce à cette correspondance, il devient possible de concevoir un texte aléatoire en commençant par n'importe quel préfixe et en choisissant aléatoirement parmi les suffixes possibles. Ensuite, la particule finale du préfixe peut être combinée avec le nouveau suffixe pour former le préfixe suivant. Le procédé est alors répété.

Par exemple, si nous commençons par le préfixe « le sable », le mot suivant doit être « sur » (c'est la seule combinaison entre ces deux termes observable dans l'extrait). Le préfixe suivant est « sable sur », donc le suffixe suivant doit être « la ». Ensuite, le préfixe suivant est « sur la » qui a pour suffixes soit « neige », soit « lampe ».

Dans cet exemple, le nombre de mots formant un préfixe vaut toujours deux, mais il est tout à fait envisageable d'entreprendre une analyse de Markov avec des préfixes dont les mots apparaissent en nombre quelconque, voire variable.

13-8-1. Exercice 13-8▲

Utiliser l'analyse de Markov pour générer du texte aléatoire est amusant, cependant, cet exercice a aussi un intérêt : la sélection de la structure des données. Dans les exercices précédents, vous deviez exercer des choix pour :

• la représentation des préfixes ;
• la représentation de la collection de suffixes possibles ;
• la représentation de la correspondance entre chaque préfixe et la collection de suffixes possibles.

La solution pour ce dernier choix à poser est simple. Un dictionnaire constitue le choix évident pour établir une correspondance entre les clés et les valeurs correspondantes.

Pour les préfixes, les options les plus évidentes sont les chaînes de caractères, les tableaux de chaînes de caractères ou les tuples de chaînes de caractères. Pour les suffixes, un tableau est une option ; un histogramme de dictionnaire en est une autre.

Comment choisir ? La première étape consiste à réfléchir aux opérations qu'il est nécessaire d'implémenter pour chaque structure de données. Pour les préfixes, nous devons pouvoir supprimer des mots du début et en ajouter à la fin. Par exemple, si le préfixe est « le sable » et que le mot suivant est « sur », il faut pouvoir former le préfixe suivant, « sable sur ». Un tableau pourrait constituer un premier choix, car il est facile d'y ajouter et d'y supprimer des éléments. Pour la collection de suffixes, les opérations à effectuer comprennent l'ajout d'un nouveau suffixe (ou l'augmentation de la fréquence d'un suffixe existant) ainsi que le choix d'un suffixe aléatoire.

L'ajout d'un nouveau suffixe est tout aussi facile dans le cas d'un tableau que dans celui d'un histogramme. Choisir un élément aléatoire dans un tableau est commode ; en choisir un dans un histogramme s'avère plus difficile à réaliser efficacement (voir l'exercice 13.7.1Exercice 13-7).

Jusqu'à présent, la facilité de mise en œuvre a été privilégiée. Cependant, d'autres facteurs interviennent dans le choix de la structure de données. L'un d'eux est le temps d'exécution. Parfois, une raison théorique permet d'espérer qu'une structure de données se montre plus rapide qu'une autre. Par exemple, nous avons vu que l'opérateur ∈ est plus rapide pour les dictionnaires que pour les tableaux, du moins lorsque le nombre d'éléments est important.

Cependant, très souvent, nul ne sait a priori quelle implémentation sera la plus rapide. Une option consiste à développer deux implémentations et à observer la meilleure. Cette approche est appelée analyse comparative (ou benchmarking). Une autre option pratique consiste à choisir la structure de données la plus facile à mettre en œuvre, puis à analyser si elle est suffisamment rapide pour l'application prévue. Si c'est le cas, il n'est pas nécessaire de chercher plus loin. Sinon, des outils comme le module Profile (voir la documentation Julia et Profileview) permettent d'identifier les blocs les plus lents d'un programme. Citons également BenchmarkTools (voir BenchmarkTools.jl) qui fournit diverses macros permettant d'automatiser les mesures de temps d'exécution sur plusieurs jeux de paramètres (aléatoires, par exemple) (33).

L'espace de stockage constitue un autre facteur à prendre en compte. Par exemple, l'utilisation d'un histogramme pour la collecte des suffixes peut prendre moins d'espace, car il suffit d'enregistrer chaque mot une seule fois, quelle que soit sa fréquence dans le texte. Dans certains cas, l'économie d'espace peut également accélérer le fonctionnement d'un programme et, à l'extrême, ce dernier peut ne pas fonctionner du tout en cas de mémoire saturée. Néanmoins, pour de nombreuses applications, l'espace mémoire reste une considération secondaire par rapport au temps d'exécution.

Une dernière réflexion : dans cette discussion, nous avons laissé entendre qu'une seule structure de données était à exploiter à la fois pour l'analyse et le développement. Parce que ces deux phases sont distinctes, il est envisageable d'utiliser une structure pour l'analyse et de la convertir ensuite en une autre pour le développement. Le gain sera net si le temps épargné pendant le développement dépasse celui consacré à la conversion.

Lors du débogage d'un programme, cinq attitudes sont à adopter en particulier lorsque le bogue est très difficile à débusquer :

la lecture examinez votre code, relisez-le avec détachement, comme si c'était le programme de quelqu'un d'autre et vérifiez ce qu'il exécute réellement ;

le fonctionnement expérimentez, en introduisant de petites modifications et en exécutant différentes versions. Souvent, si vous affichez le bon élément au bon endroit dans le programme, le problème saute aux yeux. Parfois, il faut construire un canevas ;

la réflexion prenez le temps de réfléchir. De quel type d'erreur s'agit-il : syntaxique, d'exécution ou sémantique ? Quelles informations pouvez-vous tirer des messages d'erreur ou du rendu du programme ? Quel type d'erreur pourrait causer le problème que vous constatez ? Qu'avez-vous modifié en dernier lieu, avant que le problème n'apparaisse ?(34)

la méthode du canard en plastique (rubber ducking) si vous expliquez le problème à quelqu'un d'autre, vous trouvez parfois la réponse avant même d'avoir fini de poser la question. Souvent, vous n'avez même pas besoin d'une autre personne. Vous pourriez simplement parler à un canard en plastique. Là, se trouve l'origine de la stratégie bien connue appelée « débogage par la méthode du canard en plastique »(35) ;

le « lâcher prise » à un moment donné, la meilleure chose à faire est de reculer et d'annuler les changements récents jusqu'à revenir à un programme qui fonctionne et que vous comprenez. Ensuite, une nouvelle période de reconstruction pourra commencer.

Les programmeurs débutants se trouvent parfois bloqués sur une de ces activités et oublient les autres. Chaque activité a ses propres limites. Par exemple, la lecture du code peut aider si le problème est d'ordre typographique, mais pas si le problème résulte d'un malentendu conceptuel. Si vous ne comprenez pas l'exécution de votre programme, vous pouvez le lire 100 fois et ne jamais repérer l'erreur, car celle-ci est mentale.

Faire des expériences peut aider, surtout en procédant par de petits tests simples. En revanche, si vous faites des essais sans stratégie ou sans lire votre code, vous risquez de basculer dans de la « programmation en mode aléatoire », qui consiste à faire des changements aléatoires jusqu'à ce que le programme fasse ce à quoi il est destiné. Il va sans dire que la programmation en mode aléatoire est très chronophage et sans réelle garantie de résultat.

Vous devez prendre le temps de réfléchir. Le débogage est de même essence qu'une science expérimentale. Vous devez avoir au moins une hypothèse sur la nature du problème. S'il y a deux possibilités ou plus, essayez de penser à un test discriminant.

Pour tout dire, même les meilleures techniques de débogage échouent lorsqu'il y a trop d'erreurs ou si le code que vous essayez de corriger est trop volumineux et trop complexe. Parfois, la meilleure option est de battre en retraite, en simplifiant le programme jusqu'à arriver à un code qui fonctionne et qui est parfaitement compris.

Les programmeurs débutants sont souvent réticents à rebrousser chemin parce qu'ils ne supportent pas d'effacer une ligne de code (même lorsqu'elle est erronée). Si cela vous rassure, sauvegardez votre programme dans un autre fichier avant de commencer à le décortiquer. Vous pourrez ensuite recopier un à un les blocs analysés et corrects.

Pour trouver un bogue difficile, il est nécessaire de lire, d'expérimenter, de réfléchir et parfois… de reculer. Si vous êtes bloqué sur l'une de ces activités, n'hésitez pas à essayer les autres.

déterministe terme qui se rapporte à un programme qui produit le même résultat à chaque exécution, avec les mêmes apports (voir la notion de fonction déterministe en informatique).

pseudoaléatoire terme se rapportant à une séquence de nombres qui semble être aléatoire, mais qui est conçue par un programme déterministe ;

valeur par défaut valeur donnée à un paramètre optionnel si aucun argument n'est fourni ;

outrepassement (override) remplacement d'une valeur par défaut par un argument fourni par l'utilisateur ;

analyse comparative (benchmarking) processus consistant à choisir entre les structures de données en implémentant des alternatives et en les testant sur un échantillon d'entrées possibles.

méthode du canard en plastique (rubber ducking) méthode de débogage où le programmeur explique à un objet inanimé (tel qu'un canard en plastique) son problème en le décomposant pour se rendre compte de la ou des faille(s).

13-12-1. Exercice 13-9▲

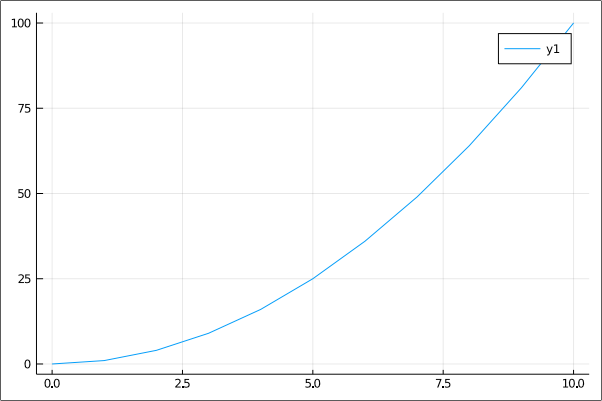
julia> using Plots
julia> x = 0:10
julia> y = x .^2
julia> plot(x, y)
julia> savefig("/home/chemin_vers_repertoire/quadratic.pdf")