Think Julia

À l'instar d'une chaîne de caractères, un tableau est une séquence de valeurs. Dans une chaîne, les valeurs sont des caractères. Dans un tableau, elles peuvent être de n'importe quel type. Les valeurs d'un tableau sont appelées des éléments (ou parfois des items).

Il existe plusieurs façons de créer un nouveau tableau. La plus simple consiste à mettre les éléments entre crochets [ ] :

julia> [10, 20, 30, 40]
4-element Array{Int64,1}:
  10
  20
  30
  40

julia> ["ici", "là", "encore", "déjà"]
julia> ["spam", 2.0, 5, [10, 20]]

La deuxième ligne du dernier encadré illustre un cas de tableau imbriqué.

Un tableau qui ne contient aucun élément est dit « vide ». Il est possible d'en créer un avec des crochets sans contenu [ ].

Comme on peut s'y attendre, il est possible d'affecter des tableaux à des variables :

julia> fromages = ["Maroilles", "Beaufort", "Ossau-iraty"];

julia> nombres = [42, 123];

julia> vide = [];

julia> print(fromages, " ", nombres, " ", vide)
["Maroilles", "Beaufort", "Ossau-iraty"] [42, 123] Any[]

La fonction typeof permet de connaître le type d'un tableau :

julia> typeof(fromages)
Array{String,1}
julia> typeof(nombres)
Array{Int64,1}
julia> typeof(vide)
Array{Any,1}

Entre les accolades, se trouvent le type et un nombre. Ce nombre indique les dimensions du tableau (un tableau simple a une seule dimension ; un tableau bidimensionnel ou matrice, deux, etc.). Le tableau vide contient des valeurs de type Any, c'est-à-dire qu'il peut contenir des valeurs de tout type.

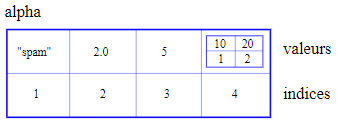
La syntaxe pour accéder aux éléments d'un tableau est la même que celle permettant d'accéder aux caractères d'une chaîne : il convient d'utiliser l'opérateur [ ]. L'expression à l'intérieur des parenthèses spécifie l'indice. Pour rappel, en Julia, les indices commencent à 1 comme indiqué dans la figure 10.2.1.

Par exemple :

julia> fromages[1] 
"Maroilles"

julia> alpha = ["spam", 2.0, 5, [10, 20]]
julia> alpha[4][2]
20

Contrairement aux chaînes, les tableaux sont non persistants (c'est-à-dire qu'ils sont modifiables). Lorsque l'opérateur [ ] apparaît à gauche d'une affectation, il identifie l'élément du tableau concerné par cette dernière :

julia> nombres[2] = 5
5
julia> print(nombres)
[42, 5]

Alors qu'il était auparavant égal à 123, le second élément de nombres vaut désormais 5.

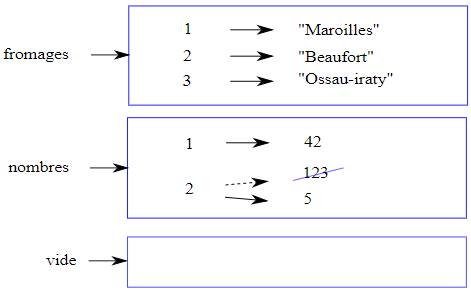
La figure 10.2.2 montre les diagrammes d'état pour fromages, nombres et vide.

Les tableaux sont représentés par des cases contenant les éléments et les indices. fromages fait référence à un tableau avec trois éléments indicés 1, 2 et 3. Le tableau nombres contient deux éléments. Le diagramme montre que la valeur du deuxième élément a été réaffectée de 123 à 5. Quant à lui, vide fait référence à un tableau sans élément.

Les indices de tableau fonctionnent de la même manière que ceux des chaînes (mais sans les mises en garde UTF-8) :

• toute expression entière peut être utilisée comme un indice. Par exemple, alpha[1+1] retourne 2.0 ;

• si vous essayez de lire ou d'écrire un élément qui n'existe pas, vous obtenez une BoundsError ;

• le mot-clé end pointe vers le dernier indice d'un tableau.

L'opérateur ∈ fonctionne également sur les tableaux :

julia> "Ossau-iraty" ∈ fromages
true
julia> "Brie" in fromages
false

Avant de parcourir un tableau, il est utile de voir comment déterminer le nombre d'éléments qui le constituent en utilisant la fonction length :

julia> length(nombres)
2
julia> length(alpha)
4

Bien qu'un tableau puisse en contenir un autre (comme c'est le cas pour alpha), le tableau imbriqué compte toujours comme un élément unique.

La manière la plus courante de parcourir les éléments d'un tableau consiste à utiliser une boucle for. La syntaxe est la même que pour les chaînes de caractères :

for fromage in fromages
    println(fromage)
end

Cela ne fonctionne bien que quand il suffit de lire les éléments du tableau. S'il est nécessaire d'en ajouter, d'en retirer ou d'en mettre à jour, il faut manipuler les indices. Une façon courante de procéder repose sur l'usage de la fonction interne eachindex :

for i in eachindex(nombres)
    nombres[i] = nombres[i] * 2
end

Cette boucle for parcourt le tableau et met à jour chaque élément. Chaque fois que la boucle est parcourue, nous obtenons l'indice de l'élément suivant. L'instruction d'affectation dans le corps utilise i pour lire l'ancienne valeur de l'élément et pour affecter la nouvelle valeur.

Une boucle for sur un tableau vide ne fait jamais tourner le corps de cette boucle :

for x in []
    println("Ceci n'arrivera pas!")
end

L'opérateur de segmentation fonctionne également avec les tableaux :

julia> t = ['a', 'b', 'c', 'd', 'e', 'f'];

julia> print(t[1:3])
['a', 'b', 'c']
julia> print(t[3:end])
['c', 'd', 'e', 'f']

L'opérateur de segmentation [:] effectue une copie de l'ensemble du tableau :

julia> print(t[:])
['a', 'b', 'c', 'd', 'e', 'f']

Les tableaux étant non persistants, il est souvent utile d'en faire une copie avant d'effectuer des opérations qui les modifient.

Un opérateur de segmentation sur le côté gauche d'une affectation peut mettre à jour plusieurs éléments d'un coup :

julia> t[2:3] = ['x', 'y'];

julia> print(t)
['a', 'x', 'y', 'd', 'e', 'f']

Plusieurs fonctions internes de Julia sont conçues pour agir sur les tableaux. Par exemple, push! ajoute un nouvel élément à la fin d'un tableau :

julia> t = ['a', 'b', 'c'];

julia> push!(t, 'd');

julia> print(t)
['a', 'b', 'c', 'd']

La fonction append! ajoute des éléments d'un second tableau à la fin d'un premier :

julia> t1= ['a', 'b', 'c'];

julia> t2= ['d', 'e'];

julia> append!(t1, t2);

julia> print(t1)
['a', 'b', 'c', 'd', 'e']

Il doit être noté que t2 n'est pas modifié au cours de cette opération.

La fonction sort! organise les éléments du tableau dans l'ordre croissant (ou alphabétique) :

julia> t = ['d', 'c', 'e', 'b', 'a'];

julia> sort!(t);

julia> print(t)
['a', 'b', 'c', 'd', 'e']

La fonction sort retourne une copie des éléments du tableau dans l'ordre :

julia> t1 = ['d', 'c', 'e', 'b', 'a'];

julia> t2 = sort(t1);

julia> print(t1)
['d', 'c', 'e', 'b', 'a']
julia> print(t2)
['a', 'b', 'c', 'd', 'e']

Pour additionner tous les nombres d'un tableau, une boucle comme celle-ci est utilisable :

function addall(t)
    total = 0
    for x in t
        total += x
    end
    total
end

La variable locale total est initialisée à 0. À chaque passage dans la boucle for, += extrait un élément du tableau et l'ajoute à total. L'opérateur += constitue un raccourci pour mettre à jour une variable. Cette déclaration d'affectation avec incrémentation,

total += x

équivaut à :

total = total + x

À chaque passage dans la boucle, total accumule la somme des éléments. Une variable utilisée de cette façon est appelée un accumulateur.

L'addition des éléments d'un tableau est une opération si courante que Julia fournit la fonction interne sum :

julia> t= [1, 2, 3, 4]
sum(t)
10

Une opération de ce type qui combine une séquence d'éléments en une seule valeur s'appelle une opération de réduction.

Souvent, il faut parcourir un tableau tout en en construisant un autre. Par exemple, la fonction suivante prend un tableau de chaînes de caractères et retourne un nouveau tableau qui contient les chaînes en majuscules :

function capitalizeall(t)
    res = []
    for s in t
        push!(res, uppercase(s))
    end
    res
end

La variable res est initialisé avec un tableau vide. À chaque passage par la boucle, l'élément suivant est ajouté à res qui, en conséquence, constitue un autre type d'accumulateur.

L'opération qu'effectue capitalizeall est parfois appelée mapping parce que cette fonction effectue une « mise en correspondance » sur chacun des éléments d'une séquence (en l'occurrence avec une conversion en majuscules).

Une autre opération courante consiste à sélectionner certains des éléments d'un tableau et à retourner un sous-tableau. Par exemple, la fonction suivante prend un tableau de chaînes de caractères et retourne un tableau qui ne contient que les chaînes en majuscules :

function onlyupper(t)
    res = []
    for s in t
        if s == uppercase(s)
            push!(res, s)
        end
    end
    res
end

Une fonction comme onlyupper agit tel un filtre puisqu'elle opère sélectivement sur certains éléments.

La plupart des opérations courantes sur les tableaux peuvent être exprimées comme une combinaison de « mise en correspondance » (mapping), de filtrage et de réduction.

Pour chaque opérateur binaire tel que ^, il y a un opérateur pointé correspondant .^ automatiquement défini pour effectuer distributivement ^ élément par élément sur les tableaux. Par exemple, [1, 2, 3] ^ 3 n'est pas défini, mais [1, 2, 3] .^ 3 est défini comme le calcul du résultat élément par élément [1^3, 2^3, 3^3] :

julia> print([1, 2, 3] .^ 3)
[1, 8, 27]

Dans Julia, toute fonction f peut être appliquée de manière distribuée à tout tableau. Par exemple, pour mettre en majuscules un tableau de chaînes de caractères, nous n'avons pas besoin d'une boucle explicite :

julia> t = uppercase.(["abc", "def", "ghi"]);

julia> print(t)
["ABC", "DEF", "GHI"]

C'est une façon élégante de créer un mapping. La fonction capitalizeall peut être mise en œuvre en une seule ligne :

function capitalizeall(t)
    uppercase.(t)
end

Il existe plusieurs façons de supprimer des éléments appartenant à un tableau. Si l'indice de l'élément à supprimer est connu, la fonction splice! est utilisable :

julia> t = ['a', 'b', 'c'];

julia> splice!(t, 2)
'b': ASCII/Unicode U+0062 (category Ll: Letter, lowercase)
julia> print(t)
['a', 'c']

splice! modifie le tableau et retourne l'élément supprimé.

pop! supprime le dernier élément d'un tableau et le retourne :

julia> t = ['a', 'b', 'c'];

julia> pop!(t)
'c': ASCII/Unicode U+0063 (category Ll: Letter, lowercase)
julia> print(t)
['a', 'b']

popfirst! supprime le premier élément et le retourne :

julia> t = ['a', 'b', 'c'];

julia> popfirst!(t)
'a': ASCII/Unicode U+0061 (category Ll: Letter, lowercase)
julia> print(t)
['b', 'c']

Les fonctions pushfirst! et push! insèrent un élément au début et à la fin d'un tableau, respectivement.

Si vous n'avez pas besoin de la valeur supprimée, vous pouvez tirer profit de la fonction deleteat! :

julia> t = ['a', 'b', 'c'];

julia> print(deleteat!(t, 2))
['a', 'c']

La fonction insert! insère un élément à un indice donné :

julia> t = ['a', 'b', 'c'];

julia> print(insert!(t, 2, 'x'))
['a', 'x', 'b', 'c']

Une chaîne est une séquence de caractères alors qu'un tableau est une séquence de valeurs. Ceci dit, un tableau de caractères n'est pas une chaîne. Pour convertir une chaîne de caractères en un tableau de caractères, il convient d'employer la fonction collect :

julia> t = collect("spam");

julia> print(t)
['s', 'p', 'a', 'm']

La fonction collect permet de décomposer une chaîne ou une autre séquence en éléments individuels.

Si vous souhaitez décomposer une chaîne de caractères en mots, vous pouvez utiliser la fonction split :(20)

julia> t = split("Au calme clair de lune triste et beau");

julia> print(t)
SubString{String}["Au", "calme", "clair", "de", "lune", "triste", "et", "beau"]

Un délimiteur (qui constitue un argument optionnel) précise le(s) caractère(s) à utiliser pour détacher les mots les uns des autres. L'exemple suivant utilise un trait d'union comme délimiteur :

julia> t = split("spam-spam-spam", '-');

julia> print(t)
SubString{String}["spam", "spam", "spam"]

La fonction join effectue l'opération inverse de split. Elle prend un ensemble de chaînes de caractères et concatène les éléments :

julia> t = ["Au", "calme", "clair", "de", "lune", "triste", "et", "beau"];

julia> s = join(t, ' ')
"Au calme clair de lune triste et beau"

Dans ce cas, le délimiteur est un caractère d'espacement. Pour concaténer des chaînes de caractères sans espace(s), il convient de ne pas spécifier de délimiteur.

Un objet est une structure de données à laquelle une variable peut se référer. Jusqu'à présent, vous pouviez utiliser indifféremment les termes « objet » et « valeur », qui constituent des séquences informatiques.

Si les déclarations d'affectation sont effectuées ainsi :

a = "banane"
b = "banane"

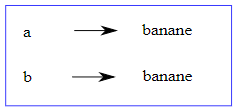
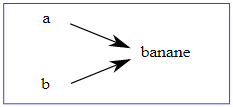
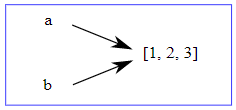
il est clair que a et b font tous deux référence à une chaîne de caractères. Cependant, a et b font-elles référence à la même chaîne ? Il existe deux états possibles illustrés dans la figure 10.10.1.

Pour vérifier si deux variables désignent le même objet, il faut utiliser l'opérateur kitxmlcodeinlinelatexdvp\equivfinkitxmlcodeinlinelatexdvp (\equiv TAB) ou ===.

julia> a = "banane"
"banane"
julia> b = "banane"
"banane"
julia> a ≡ b
true

Dans cet exemple, Julia n'a créé qu'un seul objet « chaîne de caractères ». Nous avons donc affaire au cas représenté à la sous-figure 10.10.1b.

A contrario, lorsque deux tableaux sont instanciés, nous sommes confrontés à deux objets :

julia> a = [1, 2, 3]; 

julia> b = [1, 2, 3]; 

julia> a ≡ b
false

Dans ce cas, les deux tableaux sont équivalents parce qu'ils contiennent les mêmes éléments. Toutefois, ils ne sont pas identiques parce qu'ils ne représentent pas le même objet. Ce cas est illustré dans le diagramme d'état de la figure 10.10.2.

Si deux objets sont identiques, ils sont forcément équivalents, mais, s'ils sont équivalents, ils ne sont pas nécessairement identiques.

Pour être précis, un objet a une valeur. Si nous évaluons [1, 2, 3], nous obtenons un tableau d'objets dont la valeur est une séquence d'entiers. Si un autre tableau a les mêmes éléments, on dit qu'il a la même valeur, mais il ne s'agit pas du même objet.

(21) Si a se rapporte à un objet et que nous effectuons l'affectation b = a, alors les deux variables se rapportent au même objet :

julia> a = [1, 2, 3];

julia> b = a;

julia> a ≡ b
true

Le diagramme d'état lié à cette situation est donné à la figure 10.11.1.

L'association d'une variable à un objet est un référencement. Dans cet exemple, il y a deux références au même objet, symbolisées par les deux flèches.

Un objet ayant plus d'une référence possède plus d'un nom, on dit donc que l'objet est aliasé.

Si l'objet aliasé est non persistant, les modifications apportées à un alias affectent l'autre :

julia> b[1] = 42
42
julia> print(a)
[42, 2, 3]

En revanche, pour les objets persistants comme les chaînes de caractères, l'aliasing ne constitue pas un véritable problème. Dans cet exemple (qui se réfère à la sous-figure 10.10.1a) :

a = "banane"
b = "banane"

travailler sur a n'affecte pas b.

Lorsqu'un tableau est passé en argument à une fonction, la fonction acquiert une référence au tableau, puisqu'elle y accède. Si la fonction modifie le tableau, l'appelant perçoit le changement. Par exemple, deletehead! supprime le premier élément d'un tableau :

function deletehead!(t)
    popfirst!(t)
end

Voici un exemple :

julia> letters = ['a', 'b', 'c'];

julia> deletehead!(letters);

julia> print(letters)
['b', 'c']

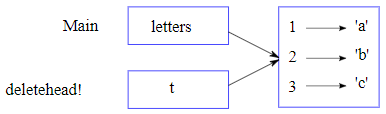
Le paramètre t et la variable letters sont des alias pour le même objet. Le diagramme de pile est donné à la figure 10.12.1.

Lorsque letters est passé à t, les variables variables (l'une globale, letters, et l'autre locale, t) se réfèrent au même tableau.

Il est important de distinguer les opérations qui modifient les tableaux et celles qui en créent de nouveaux. Par exemple, push! modifie un tableau alors que vcat en crée un nouveau.

Voici un exemple d'utilisation de push! :

julia> t1 = [1, 2];

julia> t2 = push!(t1,3);

julia> print(t1)
['1', '2', '3']

En l'espèce, t2 est un alias de t1.

À présent, voici un exemple d'utilisation de la fonction vcat :

julia> t3 = vcat(t1, [4]);

julia> print(t1)
['1', '2', '3']
julia> print(t3)
['1', '2', '3', '4']

Le résultat de vcat est un nouveau tableau. Le tableau original est inchangé.

Cette différence est importante lorsque sont rédigées des fonctions censées modifier des tableaux.

Par exemple, cette fonction baddeletehead ne supprime pas le premier élément d'un tableau :

function baddeletehead(t)
    t = t[2:end]     # erroné
end

L'opérateur de segmentation crée un nouveau tableau et l'affectation y fait référence, mais cela n'altère pas l'argument de la fonction baddeletehead en lui-même.

julia> t4 = baddeletehead(t3);

julia> print(t3)
['1', '2', '3', '4']
julia> print(t4)
['2', '3', '4']

Au début de baddeletehead, t et t3 font référence au même tableau. À la fin, t fait référence à un nouveau tableau, mais t3 pointe toujours vers le tableau original, non modifié.

Une autre manière de procéder consiste à écrire une fonction qui crée et retourne un nouveau tableau. Par exemple, tail retourne tout sauf le premier élément d'un tableau :

function tail(t)
    t[2:end]
end

Cette fonction ne modifie pas le tableau original. Voici comment elle est utilisée :

julia> letters = ['a', 'b', 'c'];

julia> rest = tail(letters);

julia> print(rest)
['b', 'c']

Une utilisation imprudente des tableaux (et des autres objets non persistants) peut entraîner de longues heures de débogage. Voici quelques pièges courants et les moyens de les éviter :

• la plupart des fonctions agissant sur les tableaux modifient ces derniers. Cette caractéristique les oppose aux fonctions traitant les chaînes de caractères, qui retournent une nouvelle chaîne de caractères et laissent l'original intact.
  Si vous avez l'habitude d'écrire du code de type chaîne de caractères de cette façon :

new_word = strip(word)

Il est tentant d'écrire un code de tableau comme celui-ci :

t2 = sort!(t1)

Parce que sort! retourne le tableau original modifié t1, t2 est un alias de t1.

• il est recommandé de choisir une manière de faire et de s'y tenir.
  Une partie du problème avec les tableaux provient du grand nombre de techniques utilisables. Par exemple, pour supprimer un élément d'un tableau, il est concevable utiliser pop!, popfirst!, delete_at ou même l'affectation d'un segment extrait du tableau. Pour ajouter un élément, il est possible de tirer parti de push!, pushfirst!, insert! ou vcat. En supposant que t soit un tableau et x un élément de ce tableau, ces méthodes sont correctes :

   

  Sélectionnez

  1.
  2.
  3.
  

  insert!(t, 4, x)
  push!(t, x)
  append!(t, [x])
  

  Alors que celles-ci sont erronées :

   

  Sélectionnez

  1.
  2.
  3.
  

  insert!(t, 4, [x])    # erroné
  push!(t, [x])         # erronée
  vcat(t, [x])          # erroné
  

• il est fortement préconisé d'effectuer des copies pour éviter les alias.
  Lors de l'utilisation d'une fonction comme sort! qui modifie l'argument, alors qu'il s'avère nécessaire de conserver également le tableau original, une copie devrait être créée :

julia> t = [3, 1, 2];

julia> t2 = t[:];     # t2 = copy(t)!

julia> sort!(t2);

julia> print(t)
[3, 1, 2]
julia> print(t2)
[1, 2, 3]

Dans cet exemple, il est judicieux de tirer avantage de la fonction intégrée sort, qui retourne un nouveau tableau trié tout en laissant intact l'original :

julia> sort!(t2);

julia> println(t)
[3, 1, 2]
julia> println(t2)
[1, 2, 3]

tableau séquence de valeurs.

élément (ou item) une des valeurs d'un tableau (ou de toute autre séquence, comme une matrice).

tableau imbriqué tableau constituant un élément d'un autre tableau.

accumulateur variable utilisée dans une boucle pour additionner (c'est-à-dire accumuler) un résultat.

déclaration d'affectation incrémentée déclaration qui met à jour la valeur d'une variable en utilisant un opérateur comme = (par exemple, +=).

opérateur point (dot) opérateur binaire qui est appliqué élément par élément à des tableaux.

syntaxe avec dot syntaxe utilisée pour appliquer une fonction par élément à un tableau quelconque.

opération de réduction modèle de traitement qui parcourt un tableau et accumule les éléments en un seul résultat.

mapping (ou mise en correspondance) modèle de traitement qui parcourt un tableau et effectue une opération sur chaque élément.

filtre modèle de traitement qui parcourt un tableau et sélectionne les éléments qui satisfont à un critère donné.

objet composant auquel une variable peut se référer. Tout objet a un type et une valeur.

équivalence propriété qu'ont deux séquences (par exemple des tableaux) à posséder les mêmes éléments de deux objets différents.

identité propriété qu'ont deux séquences (par exemple des tableaux) à désigner le même objet (ce qui implique a minima une équivalence).

référence association entre une variable et sa valeur.

aliasing cas de pseudonymie où deux ou plusieurs variables se réfèrent au même objet.

arguments facultatifs arguments figurant dans une fonction, mais dont l'usage n'est pas toujours nécessaire.

délimiteur caractère ou chaîne de caractères utilisés pour indiquer l'endroit où une chaîne doit être démariée du reste de la chaîne.

10-15-1. Exercice 10-1▲

julia> t = [[1, 2], [3], [4, 5, 6]];

julia> nestedsum(t)
21

10-15-2. Exercice 10-2▲

julia> t = [1, 2, 3];

julia> print(cumulsum(t))
2Any[1, 3, 6]

10-15-3. Exercice 10-3▲

julia> t = [1, 2, 3, 4];

julia> print(interior(t))
[2, 3]

10-15-4. Exercice 10-4▲

julia> t = [1, 2, 3, 4];

julia> interior!(t)
julia> print(t)
[2, 3]

10-15-5. Exercice 10-5▲

julia> issort([1, 2, 2])
true
julia> issort(['b', 'a'])
false

10-15-6. Exercice 10-6▲

10-15-7. Exercice 10-7▲

10-15-8. Exercice 10-8▲

10-15-9. Exercice 10-9▲

10-15-10. Exercice 10-10▲

10-15-11. Exercice 10-11▲

10-15-12. Exercice 10-12▲