Think Julia

Un dictionnaire constitue la généralisation d'un tableau. Dans un tableau, les indices doivent être des nombres entiers. Dans un dictionnaire, ils peuvent être de (presque) n'importe quel type.

Un dictionnaire contient une collection d'indices, appelés clés, et une collection de valeurs. Chaque clé est associée à une valeur unique. L'association d'une clé et d'une valeur est appelée une paire clé-valeur ou parfois un élément.

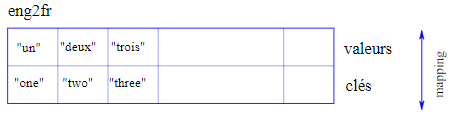
En langage informatique, un dictionnaire représente une mise en correspondance (ou mapping) ou association entre des clés et des valeurs, de sorte qu'on peut également dire que chaque clé « correspond » à une valeur (voir la figure 11.1.1). À titre d'exemple, nous allons construire un dictionnaire qui établit une correspondance entre des mots anglais et français, de sorte que les clés et les valeurs sont toutes des chaînes de caractères.

La fonction Dict crée un nouveau dictionnaire ne contenant aucun élément. Comme Dict est le nom d'une fonction intégrée, il faut éviter de l'utiliser comme nom de variable.

julia> eng2fr = Dict()
Dict{Any,Any} with 0 entries

Le type de dictionnaire est entouré d'accolades : les clés sont de type Any et les valeurs également.

Le dictionnaire est vide. Pour y ajouter des éléments, utilisons des crochets :

julia> eng2fr["one"] = "un";

Cette ligne crée un élément qui relie la clé "one" à la valeur "un". À nouveau affiché, le dictionnaire montre une paire clé-valeur. La clé est connectée à la valeur par une flèche => :

julia> eng2fr
Dict{Any,Any} with 1 entry:
   "one" => "un"

Ce format de sortie est également un format d'entrée. Par exemple, nous pouvons créer un nouveau dictionnaire comportant trois éléments :

julia> eng2fr = Dict("one" => "un", "two" => "deux", "three" => "trois")
Dict{String,String} with 3 entries:
   "one" => "un"
   "two" => "deux"
   "three" => "trois"

La figure 11.1.1 résume les attributs du dictionnaire eng2fr.

Toutes les clés et valeurs initiales sont des chaînes de caractères, de sorte qu'un Dict{String,String} est créé.

Néanmoins, cela n'a guère d'importance du fait que les éléments d'un dictionnaire ne sont jamais indicés avec des entiers. Ce sont les clés qui sont utilisées pour rechercher les valeurs correspondantes :

julia> eng2fr["two"]
"deux"

La clé "two" correspond toujours à la valeur "deux", l'ordre des éléments n'a donc pas d'importance.

Si la clé n'est pas dans le dictionnaire, Julia retourne une exception :

julia> eng2fr["four"]
ERROR: KeyError: key "four" not found

La fonction length opère également sur les dictionnaires. Elle retourne le nombre de paires clé-valeur :

julia> length(eng2fr)
3

La fonction keys retourne la collection de clés du dictionnaire :

julia> ks = keys(eng2fr);

julia> print(ks)
["two", "one", "three"]

À présent, l'opérateur ∈ est utilisable pour déterminer si un terme est une clé du dictionnaire :

julia> "one" ∈ ks 
true
julia> "un" ∈ ks 
false

Pour déterminer si une valeur appartient à un dictionnaire, la fonction values est exploitable. Elle retourne l'ensemble des valeurs, si bien qu'ensuite il est alors possible de tirer parti de l'opérateur ∈ :

julia> ks = values(eng2fr);

julia> "un" ∈ ks
true

L'opérateur ∈ utilise des algorithmes différents selon que sont traités des tableaux ou des dictionnaires. Pour les tableaux, il recherche les éléments dans l'ordre, comme dans la section 8.8Recherche dans les chaînes. Le temps de recherche s'allonge proportionnellement à la taille des tableaux.

Pour les dictionnaires, Julia utilise un algorithme appelé table de hachage (ou hash table) qui a une propriété remarquable : l'opérateur ∈ prend à peu près le même temps quel que soit le nombre d'éléments du dictionnaire.

Soit une chaîne dont il faut compter l'occurrence(22) de chaque lettre. A priori, il y a trois possibilités :

1. Créer 26 variables, une pour chaque lettre de l'alphabet, parcourir la chaîne et pour chaque caractère, incrémenter le compteur correspondant, probablement en utilisant des conditions imbriquées ;
2. Créer un tableau de 26 éléments. Ensuite, convertir chaque caractère en un nombre (en utilisant la fonction interne Int), utiliser les nombres comme indices dans le tableau et incrémenter le compteur correspondant ;
3. Créer un dictionnaire où les clés sont des caractères et où les valeurs correspondantes sont des compteurs. La première fois qu'un caractère est rencontré, le programme ajoute un élément au dictionnaire. Ensuite, la valeur d'un élément existant est incrémentée. Par exemple, pour le terme « abracadabra », la valeur de la clé « a » est 5, la valeur de la clé « b » est 2, la valeur de la clé « r » est 2, la valeur de la clé « c » est 1 et la valeur de la clé « d » est 1.

Chacune de ces options effectue le même calcul, mais avec une mise en œuvre différente.

Une implémentation est définie comme la mise en œuvre d'un calcul. Certaines s'avèrent plus performantes que d'autres. Par exemple, un des avantages de l'implémentation par dictionnaire provient du fait qu'il n'est pas nécessaire de connaître préalablement les lettres constituant la chaîne. Nous n'avons qu'une obligation : faire de la place pour insérer dans le dictionnaire les lettres détectées.

Voici à quoi pourrait ressembler le code :

function histogram(s)
    d = Dict()
    for c in s
        if c ∉ keys(d)
            d[c] = 1
        else
            d[c] += 1
        end
    end
    d
end

Le nom de la fonction est histogram, un terme associé au domaine des statistiques pour désigner une série de fréquences (c'est-à-dire d'occurrences). Comment fonctionne ce code ? Pour être concret, effectuons un appel sous la forme histogram("brontosaure") :

julia> h = histogram("brontosaure")

On passe donc la chaîne "brontosaure" à s. Ensuite, un dictionnaire vide d est créé.

Dans un premier temps, supposons que la boucle for ne contienne pas le code du test conditionnel if et qu'à sa place il n'y ait qu'une instruction println(c). Que retournerait le programme ? Il afficherait chaque lettre du mot « brontosaure » avec, chaque fois, un retour à la ligne. En effet, au premier passage, la variable c vaut 'b', au deuxième passage, elle vaut 'r' et ainsi de suite jusqu'à valoir 'e'. La boucle for parcourt donc entièrement la chaîne de caractères.

Dans un deuxième temps, on peut s'assurer de ce que contient keys(d). Pour ce faire, il suffit de remplacer l'instruction println(c) par @show keys(d). Nous devons nous attendre à 11 retours keys(d) = Any{}.

Dans un troisième temps, nous allons remplacer le test conditionnel if par ce bloc :

if c ∉ keys(d)
    d[c] = 1
    print(d[c])
else
    print("ω")
end

De sorte que la fonction prenne transitoirement cette forme :

function histogram(s)
    d = Dict()
    for c in s
        if c ∉ keys(d)
            d[c] = 1
            println(d[c])
        else
            println("ω")
        end
    end
end

Que retourne la fonction histogram("brontosaure") ? Au premier passage dans la boucle for, la variable c contient 'b'. Le code teste si 'b' se trouve parmi les clés du dictionnaire. Le dictionnaire étant vide, 'b' ne s'y trouve pas. À la ligne suivante, d['b'] effectue l'entrée de 'b' comme clé du dictionnaire et l'entier 1 est affecté à la valeur d['b'] correspondante. Le code remonte à la boucle for avec c qui, cette fois, vaut 'r' et ainsi de suite jusqu'à la cinquième lettre, 't'. La première partie de l'affichage sera donc 11111. Au passage suivant, c vaut 'o'. Cependant, il existe déjà un 'o' dans le dictionnaire et, par conséquent, le code passe au else et l'affichage devient 11111ω. Il est maintenant clair qu'à la fin nous devons obtenir un affichage tel que 11111ω111ω1.

Revenons à la fonction histogram initiale. Comme précédemment, au premier passage dans la boucle for, c vaut 'b'. Le code teste si 'b' se trouve parmi les clés du dictionnaire. Puisque ce dernier est vide, 'b' ne s'y trouve pas ; d['b'] effectue l'entrée de 'b' comme clé du dictionnaire et l'entier 1 est affecté à la valeur d['b'].

En conséquence, l'état du dictionnaire est :

keys(d) = Any['b']
d = Dict{Any,Any}('b'=> 1)

Au deuxième tour, l'état du dictionnaire passe à :

keys(d) = Any['r', 'b']
d = Dict{Any,Any}('r'=> 1,'b'=> 1)

Au cinquième tour, le dictionnaire prend cette configuration (à l'ordre des clés près) :

keys(d) = Any['t', 'n', 'o', 'r', 'b']
d = Dict{Any,Any}('t'=> 1,'n'=> 1,'o'=> 1,'r'=> 1,'b'=> 1)

Au passage suivant, le programme entre dans la partie else puisque 'o' se trouve déjà dans le dictionnaire. Sa valeur correspondante est incrémentée et devient 2. L'état du dictionnaire devient :

keys(d) = Any['t', 'n', 'o', 'r', 'b']
d = Dict{Any,Any}('t'=> 1,'n'=> 1,'o'=> 2,'r'=> 1,'b'=> 1)

In fine, l'état du dictionnaire est :

keys(d) = Any['e','r','u','a','s','o','t', 'n', 'o', 'r', 'b']
d = Dict{Any,Any}('e'=> 1,'u'=> 1,'a'=> 1,'s'=> 1,'t'=> 1,'n'=> 1,'o'=> 2,'r'=> 2,'b'=> 1)

Si vous appliquez l'appel histogram("brontosaure"), le programme retourne la valeur de d sous cette forme :

Dict{Any,Any} with 9 entries
  'n'   =>   1
  's'   =>   1
  'a'   =>   1
  'r'   =>   2
  't'   =>   1
  'o'   =>   2
  'u'   =>   1
  'e'   =>   1
  'b'   =>   1

L'histogramme indique que les lettres a, b, e, n, s, t et u apparaissent une fois ; o et r apparaissent deux fois.

Les dictionnaires possèdent une fonction appelée get qui prend une clé et une valeur par défaut. Si la clé apparaît dans le dictionnaire, get retourne la valeur correspondante. Sinon, elle retourne la valeur par défaut. Par exemple :

julia> h = histogram("brontosaure");

julia> get(h, 'a', 0)
1
julia> get(h, 'o', 0)
2
julia> get(h, 'z', 0)
0

11-2-1. Exercice 11-1▲

Les clés d'un dictionnaire peuvent être parcourues grâce à une boucle for. Par exemple, printhist affiche chaque clé et la valeur correspondante :

function printhist(h)
    for c in keys(h)
        println(c, " ", h[c])
    end
end

Voici à quoi ressemble le résultat :

julia> histogram("perroquet");

julia> printhist(h)
  u  1
  e  2
  p  1
  r  2
  o  1
  q  1
  t  1

Là encore, les clés ne sont pas dans un ordre particulier. Pour parcourir les clés dans l'ordre dans l'ordre alphabétique, la combinaison des fonctions sort et collect se révèle pratique :

julia> for c in sort(collect(keys(h)))
            println(c, " ", h[c])
           end
  e  2
  o  1
  p  1
  q  1
  r  2
  u  1
  t  1

Avec un dictionnaire d et une clé k, il est facile de trouver la valeur correspondante v = d[k]. Cette opération est appelée une recherche directe (ou lookup).

Ceci dit, comment procéder si nous disposons d'une valeur v et que nous souhaitons trouver sa clé k ? Ici, nous sommes confrontés à deux problèmes :

1. Premièrement, il peut y avoir plus d'une clé qui correspond à la valeur v (par exemple, dans le cas du tableau d associé à « brontosaure », à la valeur « 2 » correspondaient les clés 'o' et 'r') ;

2. Deuxièmement, il n'y a pas d'astuce simple pour effectuer une recherche inverse (ou reverse lookup).

Voici une fonction qui prend une valeur et retourne la première clé qui correspond à cette valeur :

function reverselookup(d, v)
    for k in keys(d) 
        if d[k] == v
            return k
        end 
    end
    error("LookupError")
end

Cette fonction est un exemple de schéma de recherche inverse, mais elle utilise une fonction error non encore abordée jusqu'ici. La fonction error est exploitée pour produire une ErrorException qui interrompt le flux de contrôle normal. Dans ce cas, elle affiche le message "LookupError", indiquant qu'une clé n'existe pas.

Si le programme arrive à la fin de la boucle, cela signifie que v n'est pas une valeur du dictionnaire. En conséquence, le programme émet une exception.

Voici un exemple de recherche inversée réussie :

julia> h = histogram("magnifique");

julia> key = reverselookup(h, 2) 
'i': ASCII/Unicode U+0069 (category Ll: Letter, lowercase)

et voici un cas qui a échoué :

julia> key = reverselookup(h, 3) 
ERROR: LookupError

Quand une exception se produit, l'effet est le même que lorsque Julia en émet une : une trace de pile (ou stacktrace) et un message d'erreur sont affichés.

Julia propose un moyen optimisé de faire une recherche inversée : findall(isequal(3), h).

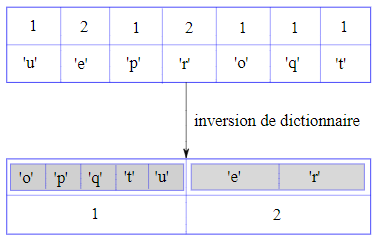
Les tableaux peuvent constituer des valeurs au sein d'un dictionnaire. Supposons un dictionnaire qui fait correspondre des lettres à des occurrences (voir section 11.2Dictionnaires en tant que collections de compteurs). On peut vouloir l'inverser, c'est-à-dire créer un dictionnaire qui fait correspondre des occurrences (en tant que clés) à des lettres (en tant que valeurs). Comme plusieurs lettres peuvent présenter la même occurrence, celles-ci peuvent être groupées, selon leur occurrence, sous forme de tableaux et ces tableaux peuvent devenir des valeurs dans le dictionnaire inversé.

La figure 11.5.1 permet de visualiser l'inversion d'un tableau (en l'espèce, l'histogramme du mot « perroquet »). Les zones grisées de la figure correspondent à deux tableaux constituant les deux valeurs du dictionnaire inversé.

Voici une fonction permettant d'inverser un dictionnaire :

function invertdict(d) 
    inverse = Dict()
    for key in keys(d)
        val = d[key]
        if val ∉ keys(inverse)
            inverse[val] = [key] 
        else 
            push!(inverse[val], key)
        end
    end 
    inverse
end

À chaque fois, dans la boucle, key récupère une clé à partir de d pendant que val récupère la valeur correspondante. Si val n'est pas dans inverse, cela signifie qu'elle n'a pas été détectée auparavant. En conséquence, un nouvel élément est créé et initialisé avec un singleton (un tableau qui contient un seul élément). Si cette valeur a été repérée auparavant, la clé qui lui correspond est ajoutée au tableau à l'aide de la fonction push!.

Voici un exemple :

julia> hist = histogram("perroquet");

julia> inverse = invertdict(hist) 
Dict{Any,Any} with 2 entries: 
   2 => ['e', 'r'] 
   1 => ['u', 'p', 'o', 'q', 't']

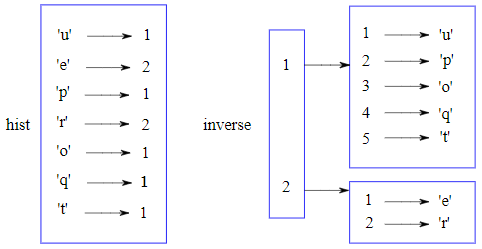
La figure 11.5.2 reprend les diagrammes d'état associés à hist et inverse. Un dictionnaire est représenté sous la forme d'un cadre contenant des paires clé-valeur (que ces valeurs soient des entiers, des flottants ou des chaînes de caractères). Pour conserver la simplicité de lecture des diagrammes, les tableaux sont disposés dans des cadres à l'extérieur de ceux associés au dictionnaire.

Si vous avez quelque peu manié la fonction fibonacci de la section 6.7Un exemple supplémentaire, vous avez remarqué que plus le nombre passé en argument est grand, plus la fonction prend de temps à effectuer le calcul. De surcroît, la durée d'exécution augmente de plus en plus rapidement.

Pour comprendre pourquoi, considérons la figure 11.6.1 qui montre le graphe d'appel pour fibonacci avec n = 4 :

Un graphe d'appel comporte un ensemble de cadres associés à une (ou des) fonction(s), avec des flèches reliant chaque cadre aux cadres des fonctions qu'il appelle. En haut du graphique, fibonacci avec n = 4 appelle fibonacci avec n = 3 et n = 2, et fibonacci avec n = 3 appelle fibonacci avec n = 2 et n = 1. Et ainsi de suite.

Il est facile de dénombrer les appels à fibonacci(0) et fibonacci(1) et de conclure à l'inefficacité de cette solution.

Un moyen de résoudre ce problème consiste à garder une trace des valeurs déjà calculées en les enregistrant dans un dictionnaire. Une valeur calculée précédemment et stockée pour une utilisation ultérieure s'appelle un mémo. Voici une version « mémo » de fibonacci :

known = Dict(0=>0, 1=>1)

function fibonacci(n)
    if n ∈ keys(known)
        return known[n] 
    end 
    res = fibonacci(n-1) + fibonacci(n-2)
    known[n] = res
    res
end

known est un dictionnaire qui garde la trace des nombres de la suite de Fibonacci déjà calculés. Il commence par deux éléments : la clé 0 est associée à la valeur 0 et la clé 1 à la valeur 1.

Chaque fois que la fonction fibonacci est appelée, elle vérifie known. Si le résultat est déjà dans le dictionnaire, il est rappelé immédiatement. Sinon, fibonacci calcule la nouvelle valeur, l'ajoute au dictionnaire et la retourne.

À l'exécution, cette version de fibonacci s'avère beaucoup plus rapide que l'originale.

Dans l'exemple précédent, known est créé en dehors de la fonction. Ce dictionnaire appartient donc à la fonction Main. Les variables dans Main sont dites globales, car elles sont accessibles depuis n'importe quelle fonction. Contrairement aux variables locales qui disparaissent lorsque leur fonction se termine, les variables globales persistent d'un appel de fonction à l'autre.

Il est courant d'utiliser des variables globales pour les drapeaux (flags), c'est-à-dire des variables booléennes qui indiquent si une condition est vraie (ou fausse). Par exemple, certains programmes utilisent un drapeau verbose pour contrôler le niveau de détail de la sortie :

verbose = true

function example1()
    if verbose 
        println("Running example1")
    end 
end

La réaffectation d'une variable globale n'entraîne pas la modification de cette dernière. L'exemple suivant est censé déterminer si la fonction (example2) a été appelée :

been_called = false

function example2() 
    been_called = true      # ERRONÉ 
end

À l'exécution, nous constatons que la valeur de been_called ne change pas. Le problème vient de ce qu'example2 crée une nouvelle variable locale appelée been_called. La variable locale disparaît lorsque la fonction se termine. Par conséquent, cela n'affecte pas la variable globale.

Pour conférer le caractère global à une variable se trouvant à l'intérieur d'une fonction, il est nécessaire de placer le terme global immédiatement devant le nom de la variable :

been_called = false

function example2()
    global been_called
    been_called = true
end

Cette déclaration globale transmet à l'interpréteur une information signifiant : « Dans cette fonction, quand nous disons been_called, nous désignons la variable globale ; ne créez pas de variable locale ». Ainsi, quand, à l'intérieur de la fonction, true est affecté à been_called, cela affecte la variable globale.

Voici un exemple qui tente erronément de mettre à jour une variable globale :

count = 0

function example3()
    count = count + 1     # ERRONÉ 
end

À l'exécution, Julia retourne un message d'erreur :

julia> example3() 
ERROR: UndefVarError: count not defined

Julia suppose que count est locale et que vous en prenez connaissance avant de modifier sa valeur. À nouveau, la solution est de déclarer count comme variable globale.

count = 0

function example3()
    global count
    count += 1
end

Si une variable globale fait référence à une séquence non persistante (comme un tableau ou un dictionnaire), il est possible de modifier les valeurs de cette séquence sans déclarer la variable comme étant globale :

known = Dict(0=>0, 1=>1)

function example4() 
    known[2] = 1
end

Par conséquent, il est admissible d'ajouter, supprimer et remplacer des éléments d'un tableau ou d'un dictionnaire global. Cependant, la réaffectation de la variable au sein d'une fonction requiert une déclaration en tant que variable globale :

known = Dict(0=>0, 1=>1)

function example5() 
    global known 
    known = Dict()
end

Pour des raisons de performance, il est judicieux d'attribuer le mot-clé const à une variable globale. De cette manière, il devient impossible de la réaffecter. Si une variable globale const se réfère à une séquence non persistante, il reste néanmoins possible d'en modifier la valeur.

const known = Dict(0=>0, 1=>1)

function example4() 
    known[2] = 1 
end

Lorsqu'on travaille avec des jeux de données volumineux, il peut devenir difficile de déboguer en affichant et en vérifiant le résultat manuellement. Voici quelques suggestions pour le débogage de grands jeux de données :

• réduire la taille de l'entrée :
  si possible, réduire la taille du jeu de données. Par exemple, si un programme lit un fichier texte, on peut commencer par les 10 premières lignes, voire — si c'est possible avec le plus petit échantillon sur lequel des erreurs sont identifiables. Il est fortement conseillé de ne pas éditer les fichiers eux-mêmes, mais plutôt de modifier le programme afin qu'il ne lise que les n premières lignes.
  S'il y a une erreur, il convient de réduire n à la plus petite valeur qui révèle l'erreur. Par la suite, la valeur de n peut être augmentée progressivement à mesure que sont détectées et corrigées les erreurs ;
• vérifiez les résumés et les types :
  au lieu d'afficher et de vérifier l'ensemble des données, il faut penser à afficher les résumés de données : par exemple, le nombre d'éléments dans un dictionnaire ou le total d'un tableau de nombres.
  Une cause fréquente d'erreurs d'exécution tient en une valeur dont type est erroné. Pour déboguer ce type d'erreur, il suffit souvent d'afficher le type d'une valeur ;
• rédigez des vérifications automatiques :
  parfois, il est habile d'écrire un peu de code pour vérifier automatiquement la présence d'erreurs. Par exemple, si la moyenne d'un tableau de nombres est calculée, on peut aisément vérifier que le résultat n'est pas supérieur au plus grand élément du tableau ou inférieur au plus petit. Il s'agit là d'une « vérification de bon sens ».
  Un autre type de contrôle consiste à comparer les résultats de deux calculs différents pour vérifier qu'ils sont cohérents. Ici, il est question d'une « vérification de cohérence » ;
• formater les messages émis :
  le formatage des messages de débogage peut aider à repérer une erreur. Nous en avons vu un exemple dans la section 6.9Débogage. Là encore, le temps investi à construire un canevas peut considérablement réduire le temps de débogage.

mapping (association ou mise en correspondance) relation dans laquelle chaque élément d'un ensemble correspond à un élément d'un autre ensemble.

dictionnaire séquence permettant une mise en correspondance de clés avec leur valeur.

paire clé-valeur représentation de la mise en correspondance (mapping) d'une clé à une valeur.

item dans un dictionnaire, synonyme d'une paire clé-valeur.

clé objet qui apparaît dans un dictionnaire comme la première partie d'une paire clé-valeur.

valeur objet qui apparaît dans un dictionnaire comme la deuxième partie d'une paire clé-valeur. Ce terme est plus spécifique que notre utilisation précédente du terme « valeur ».

implémentation mise en œuvre d'un calcul.

table de hachage (hash table) algorithme utilisé pour mettre en œuvre les dictionnaires en Julia.

fonction de hachage (hash function) fonction utilisée par une table de hachage pour calculer l'emplacement d'une clé.

recherche directe (lookup) opération du dictionnaire qui prend une clé et trouve la valeur correspondante.

recherche inversée (reverse lookup) opération sur un dictionnaire qui prend une valeur et trouve une ou plusieurs clés qui y correspondent.

singleton tableau (ou toute autre séquence) avec un seul élément.

graphe d'appel diagramme qui montre chaque cadre créé pendant l'exécution d'un programme, avec une flèche de chaque appelant à chaque appelé.

mémo valeur calculée et enregistrée pour éviter tout calcul futur redondant.

variable globale variable définie dans Main, en dehors de toute autre fonction. Les variables globales sont accessibles à partir de n'importe quelle fonction.

déclaration globale déclaration qui établit le nom d'une variable globale.

drapeau (flag ou fanion) variable booléenne utilisée pour indiquer si une condition est vraie.

déclaration énoncé tel que le mot global qui renseigne l'interpréteur sur une variable.

constante globale constante définie dans Main et ne pouvant être réaffectée.

11-10-1. Exercice 11-2▲

11-10-2. Exercice 11-3▲

11-10-3. Exercice 11-4▲

11-10-4. Exercice 11-5▲

11-10-5. Exercice 11-6▲

11-10-6. Exercice 11-7▲