12. Tuples▲
Ce chapitre présente un autre type intégré, les tuples(24). Par la suite, il montre comment les tableaux, les dictionnaires et les tuples peuvent être couplés. Nous présentons également une fonction utile pour les tableaux à arguments multiples ainsi que pour les opérateurs d'agrégation et de dispersion.
Il n'y a pas de consensus sur prononciation de « tuple ». Vous pouvez écouter comment prononcer ce mot en anglais sur ce site. Il semble qu'il n'y ait pas de prononciation française recommandée.
12-1. Les tuples sont persistants▲
Un tuple est une séquence de valeurs. Celles-ci peuvent être de type quelconque et elles sont indexées par des entiers, de sorte que, à cet égard, les tuples ressemblent beaucoup aux tableaux. La différence notoire est que les tuples sont persistants (immutable, en anglais). Chaque élément peut avoir son propre type (nombres, chaînes de caractères, tableaux, dictionnaires, tuples).
Syntaxiquement, un tuple est une liste de valeurs séparées par des virgules :
2.
julia> t = 'a', 'b', 'c', 'd', 'e'
('a', 'b', 'c', 'd', 'e')
Sans que cela soit nécessaire, il est courant de mettre les tuples entre parenthèses :
2.
julia> t = ('a', 'b', 'c', 'd', 'e')
('a', 'b', 'c', 'd', 'e')
Pour créer un tuple avec un seul élément, il est nécessaire de ponctuer avec une virgule :
2.
3.
4.
julia> t = ('a',)
('a',)
julia> typeof(t)
Tuple{Char}
Une valeur entre parenthèses sans virgule finale n'est pas un tuple :
2.
3.
4.
julia> t2 = ('a')
'a': ASCII/Unicode U+0061 (category Ll: Letter, lowercase)
julia> typeof(t2)
Char
Une autre manière de créer un tuple consiste à employer la fonction interne tuple. Sans aucun argument, elle crée un tuple vide :
2.
julia> tuple()
()
Si plusieurs arguments sont fournis, le résultat est un tuple incorporant tous les arguments donnés :
2.
julia> t3 = tuple(1, 'a', pi)
(1, 'a', 𝜋 = 3.1415926535897...)
Comme tuple est le nom d'une fonction interne, il faut éviter de l'utiliser comme nom de variable.
La plupart des opérateurs agissant sur les tableaux fonctionnent également sur des tuples. L'opérateur crochet [] indice tout élément d'un tuple :
2.
julia> t[2:4]
('b', 'c', 'd')
Cependant, comme les tuples sont persistants, vouloir en modifier un élément conduit à une erreur :
2.
julia> t[1] = ('A')
ERROR: MethodError: no method matching setindex!(::NTuple{5,Char}, ::Char, ::Int64)
Les opérateurs relationnels agissent sur les tuples comme avec d'autres séquences. Julia commence par comparer le premier élément de chaque séquence. S'ils sont égaux, Julia passe aux éléments suivants et ainsi de suite jusqu'à trouver des éléments qui diffèrent. Les éléments ultérieurs ne sont pas pris en compte (même s'il s'agit, par exemple, de grands nombres).
2.
3.
4.
julia> (0, 1, 2) < (0, 3, 4)
true
julia> (0, 1, 2000000) < (0, 3, 4)
true
12-2. Affectation des tuples▲
Il est souvent utile d'échanger les valeurs de deux variables. Dans le cas des affectations classiques, il est nécessaire utiliser une variable temporaire. Par exemple, pour permuter a et b :
2.
3.
temp = a
a = b
b = temp
Cette solution est remplacée par l'affectation de tuples qui s'avère plus élégante :
a, b = b, a
Le membre de gauche de l'affectation est un tuple de variables, alors que le membre de droite est un tuple d'expressions. Chaque valeur est attribuée à sa variable respective. Toutes les expressions du membre de droite sont évaluées avant toute affectation.
Par ailleurs, le nombre de variables du membre de gauche doit être inférieur au nombre de valeurs du membre de droite :
2.
3.
4.
julia> (a, b) = (1, 2, 3)
(1, 2, 3)
julia> a, b, c = 1, 2
ERROR: BoundsError: attempt to access (1, 2) at index [3]
Plus généralement, le membre de droite peut être tout type de séquence (chaîne, tableau ou tuple). Par exemple, pour séparer une adresse électronique en un nom d'utilisateur et un domaine, vous pouvez écrire(25) :
2.
3.
4.
5.
6.
julia> addr = "jules.cesar@rome.spqr"
jules.cesar@rome
julia> uname, domain = split(addr, '@')
2-element Array{SubString{String},1}:
"jules.cesar"
"rome.spqr"
La valeur de retour de split est un tableau à deux éléments : le premier élément est attribué à uname, le second à domain. Si le séparateur avait été '.', Julia aurait affiché trois chaînes.
12-3. Les tuples en tant que valeurs retournées▲
À vrai dire, une fonction ne peut retourner qu'une seule valeur. Toutefois, si la valeur est un tuple, l'effet est le même que si elle retournait plusieurs valeurs. Par exemple, soit deux entiers dont on veut obtenir par division le quotient et le reste. Comme il est inefficace de calculer x ÷ y puis x % y, il est préférable de réaliser ces opérations simultanément.
La fonction interne divrem qui prend deux arguments retourne un tuple de deux valeurs, le quotient et le reste. Le résultat est enregistrable sous forme de tuple :
2.
julia> t = divrem(7, 3)
(2, 1)
Il est aussi possible d'utiliser l'affectation des tuples pour enregistrer les éléments séparément :
2.
3.
4.
5.
julia> q, r = divrem(7, 3);
julia> @show q r;
q = 2
r = 1
Voici un exemple de fonction retournant un tuple :
2.
3.
function minmax(t)
minimum(t), maximum(t)
end
maximum et minimum sont des fonctions internes qui identifient les éléments les plus petits et les plus grands d'une séquence. minmax calcule les deux et retourne un tuple de deux valeurs. La fonction interne extrema est plus efficace.
12-4. Tuples et arguments multiples▲
Les fonctions peuvent prendre un nombre variable d'arguments. Un nom de paramètre qui se termine par trois points consécutifs (...) agrège les arguments dans un tuple. Par exemple, printall prend un nombre quelconque d'arguments et les affiche :
2.
3.
function printall(args...)
println(args)
end
Le nom du paramètre d'agrégation est libre, quoique le terme args soit conventionnel. Voici comment procède la fonction :
2.
julia> printall(1, 2.0, '3')
(1, 2.0, '3')
À l'agrégation s'oppose la dispersion(26). Soit une séquence de valeurs qu'on souhaite passer à une fonction sous forme d'arguments multiples, il est alors possible d'utiliser l'opérateur ... . Par exemple, divrem prend exactement deux arguments, mais cette fonction ne peut pas manipuler directement de tuples :
2.
3.
julia> t = (7, 3);
julia> divrem(t)
ERROR: MethodError: no method matching divrem(::Tuple{Int64,Int64})
En revanche, il est envisageable de disperser le tuple :
2.
julia> divrem(t...)
(2, 1)
De nombreuses fonctions internes utilisent des tuples à arguments en nombre variable. C'est le cas de max et min :
2.
julia> max(1, 2, 3)
3
En revanche la fonction sum ne traite pas les tuples :
2.
julia> sum(1, 2, 3)
ERROR: MethodError: no method matching sum(::Int64, ::Int64, ::Int64)
12-4-1. Exercice 12-1▲
Écrivez une fonction appelée sumall qui prend un nombre quelconque d'arguments et retourne leur somme.
12-5. Tableaux et tuples▲
zip est une fonction interne qui prend deux ou plusieurs séquences et retourne une collection de tuples où chacun contient un élément de chaque séquence. Le nom de la fonction fait référence à une fermeture éclair.
Cet exemple permet de « zipper » une chaîne et un tableau :
2.
3.
4.
5.
julia> s = "abc";
julia> t = [1, 2, 3];
julia> zip(s, t)
zip("abc", [1, 2, 3])
Le résultat est un objet zip capable d'itérer(27) à travers les paires(28). L'utilisation la plus courante de zip se rencontre dans une boucle :
2.
3.
4.
5.
6.
julia> for pair in zip(s, t)
println(pair)
end
('a', 1)
('b', 2)
('c', 3)
Un objet zip est une espèce d'itérateur agissant sur une séquence. D'une certaine manière, les itérateurs sont similaires aux tableaux, mais, contrairement à ces derniers, il n'est pas possible d'utiliser les indices pour sélectionner un élément donné de l'itérateur.
Afin d'utiliser des opérateurs et des fonctions de tableau, il est astucieux d'utiliser un objet zip pour créer un tableau :
2.
3.
4.
5.
julia> collect(zip(s, t))
3-element Array{Tuple{Char,Int64},1}:
('a', 1)
('b', 2)
('c', 3)
Le résultat obtenu est un tableau de tuples. Dans cet exemple, chaque tuple contient un caractère de la chaîne et l'indice correspondant du tableau.
Si les séquences ne sont pas de même longueur, la plus courte détermine la taille du résultat.
2.
3.
4.
5.
6.
julia> collect(zip("Yann", "Le Cun"))
4-element Array{Tuple{Char,Char},1}:
('Y', 'L')
('a', 'e')
('n', ' ')
('n', 'C')
L'affectation des tuples est exploitable dans une boucle for pour parcourir un ensemble des tuples :
2.
3.
4.
5.
6.
7.
8.
julia> t = [('a', 1), ('b', 2), ('c', 3)];
julia> for (letter, number) in t
println(number, " ", letter)
end
1 a
2 b
3 c
À chaque fois, Julia sélectionne le tuple suivant dans le tableau et attribue les éléments à letter et number. Les parenthèses autour de (letter, number) sont obligatoires.
En combinant zip, for et l'affectation de tuples, on obtient une expression utile pour parcourir deux (voire plusieurs) séquences simultanément. Par exemple, hasmatch prend deux séquences, t1 et t2, et retourne true s'il y a un indice i tel que t1[i] == t2[i] :
2.
3.
4.
5.
6.
7.
8.
function hasmatch(t1, t2)
for (x, y) in zip(t1, t2)
if x == y
return true
end
end
false
end
S'il faut parcourir les éléments d'une séquence et leurs indices, la fonction interne enumerate s'avère utile :
2.
3.
4.
5.
6.
julia> for (index, element) in enumerate("abc")
println(index, " ", element)
end
1 a
2 b
3 c
Le résultat de la fonction enumerate est un objet recensé qui parcourt une séquence de paires. Chaque paire contient un indice (à partir de 1) et un élément de la séquence traitée.
12-6. Dictionnaires et tuples▲
Les dictionnaires peuvent être utilisés comme des itérateurs qui permettent de parcourir les paires clé-valeur. Nous pouvons y recourir dans une boucle for de ce type :
2.
3.
4.
5.
6.
7.
8.
julia> d = Dict('a'=>1, 'b'=>2, 'c'=>3);
julia> for (key, value) in d
println(key, " ", value)
end
a 1
c 3
b 2
Comme on peut s'y attendre, les paires clé-valeur ne sont pas classées de manière ordonnée.
Inversement, un tableau de tuples est utilisable pour initialiser un nouveau dictionnaire :
2.
3.
4.
5.
6.
7.
julia> t = [('a', 1), ('c', 3), ('b', 2)];
julia> d = Dict(t)
Dict{Char,Int64} with 3 entries:
'a'=> 1
'c'=> 3
'b'=> 2
En combinant Dict et zip, on accède à un procédé concis de création d'un dictionnaire :
2.
3.
4.
5.
julia> d = Dict(zip("abc", 1:3))
Dict{Char,Int64} with 3 entries:
'a' => 1
'c' => 3
'b' => 2
Il est courant d'utiliser les tuples comme clés dans les dictionnaires. Par exemple, un annuaire téléphonique peut établir une correspondance entre des paires « nom — prénom » d'une part et de l'autre des numéros de téléphone. En supposant que nous ayons défini last (pour le nom de famille), first (pour le prénom) et number, nous pourrions écrire :
directory[last, first] = number
L'expression entre crochets est un tuple. Parcourir ce dictionnaire peut se faire via l'affectation des tuples.
2.
3.
for ((last, first), number) in directory
println(first, " ", last, " ", number)
end
Cette boucle parcourt les paires clé-valeur dans directory, ces paires étant des tuples. Elle attribue les éléments de la clé dans chaque tuple à last et first ainsi que la valeur à number. Ensuite, elle affiche le nom et le numéro de téléphone correspondant.
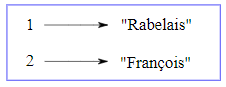
Il existe deux façons de représenter les tuples dans un diagramme d'état. La version détaillée montre les indices et les éléments tels qu'ils apparaissent dans un tableau. Par exemple, le tuple ("Rabelais", "François") apparaîtra comme dans la figure 12.6.1.
|
|
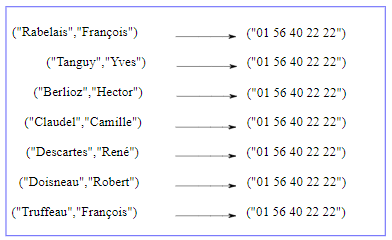
Cependant, dans un diagramme plus étendu, il est pratique d'omettre les détails. Par exemple, un diagramme de l'annuaire téléphonique peut apparaître comme dans la figure 12.6.2.
Ici, les tuples sont représentés en utilisant la syntaxe de Julia comme raccourci graphique(29).
|
|
12-7. Séquences de séquences▲
Notre attention s'est portée sur les tableaux de tuples. Néanmoins, presque tous les exemples de ce chapitre fonctionnent également avec des tableaux de tableaux, des tuples de tuples et des tuples de tableaux. Pour éviter d'énumérer les combinaisons possibles, il est parfois plus facile de parler de « séquences de séquences ».
Dans de nombreux contextes, les différents types de séquences (chaînes de caractères, tableaux et tuples) peuvent être utilisés de manière interchangeable. Alors, comment choisir l'une d'entre elles plutôt que les autres ?
Tout d'abord, les chaînes de caractères sont plus limitées que les autres séquences, car les éléments doivent absolument être des caractères. Elles sont également persistantes. S'il faut pouvoir modifier les caractères d'une chaîne (plutôt que d'en créer une nouvelle), un tableau de caractères est plus pratique.
Les tableaux sont plus courants que les tuples, principalement parce qu'ils sont non persistants. Malgré cela, il existe quelques cas où les tuples leur sont préférés :
- dans certains contextes, comme une instruction de retour, il est syntaxiquement plus simple de créer un tuple qu'un tableau ;
-
quand une séquence est passée en argument d'une fonction, l'utilisation de tuples réduit le risque de comportements inattendus dû à l'aliasing ;
- pour des raisons de performance, le compilateur pouvant se focaliser sur le type.
Comme les tuples sont persistants, ils ne fournissent pas de fonctions telles que sort! et reverse! qui modifient les tableaux existants. Cependant, Julia fournit la fonction interne sort qui prend un tableau et retourne un nouveau tableau avec les mêmes éléments triés et ordonnés. Julia met aussi à disposition la fonction reverse qui prend une séquence quelconque et retourne une séquence du même type dans l'ordre inverse.
12-8. Débogage▲
Les tableaux, les dictionnaires et les tuples sont des exemples de structures de données. Plus loin dans ce document, nous abordons les structures de données composites comme des tableaux de tuples ou des dictionnaires qui contiennent des tuples comme clés et des tableaux comme valeurs. Les structures de données composites sont utiles. Malheureusement, elles sont sujettes à des erreurs de forme, c'est-à-dire des erreurs causées lorsqu'une structure de données présente un mauvais type, une mauvaise taille ou une mauvaise structure. Par exemple, si vous vous attendez à un tableau avec un entier et que vous recevez un entier ordinaire (c'est-à-dire non incorporé à un tableau), la structure de données ne fonctionnera pas.
Julia permet d'attacher un type aux éléments d'une séquence. La manière de procéder est détaillée dans le chapitre 17Dispatch multiple. Spécifier le type contribue à éliminer beaucoup d'erreurs de forme.
12-9. Glossaire▲
tuple séquence persistante d'éléments où chacun de ceux-ci peut avoir son propre type.
affectation de tuples affection avec une séquence sur le membre de droite et un tuple de variables sur le membre de gauche. Le membre de droite est d'abord évalué et ses éléments sont ensuite affectés aux variables du membre de gauche.
agrégation opération consistant à assembler un tuple d'argument de longueur variable.
dispersion opération consistant à traiter une séquence comme une liste d'arguments.
objet zip résultat de l'appel de la fonction interne zip. Objet qui itère à travers une séquence de tuples.
itérateur objet qui peut itérer à travers une séquence, mais qui ne fournit pas d'opérateurs ni de fonctions de tableau.
structure de données collection de valeurs connexes, souvent organisées en tableau, dictionnaires, tuples, etc.
erreur de forme erreur causée par une valeur ayant une forme incorrecte, c'est-à-dire un type ou une taille incorrecte.
12-10. Exercices▲
12-10-1. Exercice 12-2▲
Écrivez une fonction appelée mostfrequent qui prend une chaîne de caractères et affiche les lettres par ordre décroissant d'occurrence. Trouvez des échantillons de texte de plusieurs langues différentes et voyez comment la fréquence des lettres varie d'une langue à l'autre. Comparez vos résultats avec les tableaux répertoriés sur les sites anglais et français.
12-10-2. Exercice 12-3▲
Encore quelques anagrammes…
-
Écrivez un programme qui lit une liste de mots à partir d'un fichier (voir la section 9.1Lecture de listes de mots) et imprime les ensembles de mots qui sont des anagrammes. Voici un échantillon de ce à quoi la sortie pourrait ressembler avec le fichier mots_FR.txt :
Sélectionnez1.
2.
3.
4.["mari","mira","rami","rima"] ["marche","charme"] ["mienne","ennemi"] ["alimenter","terminale"]Si vous voulez construire un dictionnaire qui établit une correspondance entre une collection de lettres et une série de mots qui peuvent être orthographiés avec ces lettres, comment pouvez-vous représenter la collection de lettres de manière à ce qu'elle puisse servir de clé ?
-
Modifiez le programme précédent de manière à ce qu'il affiche les anagrammes par ordre décroissant de taille.
- Au jeu de Scrabble, un « scrabble(30) » est un coup où les sept lettres de votre grille sont posées en les combinant à une lettre du tableau, pour former un mot de huit lettres. Quelle collection de 8 lettres forme le plus de « scrabble » possible ?
12-10-3. Exercice 12-4▲
Deux mots forment une paire de métathèse(31) si vous pouvez transformer l'un en l'autre en échangeant deux lettres. Par exemple, « converser » et « conserver ». Écrivez un programme qui trouve toutes les paires de métathèse dans le dictionnaire.
Ne testez pas toutes les paires de mots et ne testez pas tous les échanges possibles.
Remarque. Cet exercice est inspiré d'un exemple se trouvant sur le site« Puzzlers.org ».
12-10-4. Exercice 12-5▲
Voici un autre exemple tiré du site Car Talk.
« Quel est le mot anglais le plus long, qui reste un mot anglais valide, car vous enlevez ses lettres une à une ?
Maintenant, les lettres peuvent être enlevées à l'une ou l'autre extrémité, ou au milieu, mais vous ne pouvez pas réarranger les lettres. Chaque fois que vous laissez tomber une lettre, vous vous retrouvez avec un autre mot anglais. Si vous faites cela, vous finirez par avoir une lettre et ce sera aussi un mot anglais - un mot que l'on trouve dans le dictionnaire. Je veux savoir quel est le mot le plus long et combien de lettres il comporte.
Je vais vous donner un petit exemple modeste : Sprite. D'accord ? On commence par sprite, on enlève une lettre, une de l'intérieur du mot, on enlève le r, et on se retrouve avec le mot spite, puis on enlève le e à la fin, on se retrouve avec spit, on enlève le s, on se retrouve avec pit, it et I. »
Écrivez un programme pour trouver tous les mots qui peuvent être réduits de cette façon, puis trouvez le plus long.
Le commentaire est associé à la langue anglaise. Utilisez mots_FR.txt (voir la section 9.1Lecture de listes de mots). Cet exercice est un peu plus difficile que la plupart des autres, aussi voici quelques suggestions :
- Vous pourriez écrire une fonction qui prend un mot et calcule un tableau de tous les mots qui peuvent être formés en enlevant une lettre. Ce sont les « mots-fils » ;
- Récursivement, un mot est réductible si l'un de ses fils est réductible. Comme cas de base, vous pouvez considérer la chaîne vide comme réductible ;
- La chaîne vide peut être additionnée au dictionnaire ;
- Pour améliorer la performance de votre programme, vous pouvez utiliser un « mémo » pour les mots connus pour être réductibles.