Think Julia

Dans ce cas, l'appel d'une fonction retourne une valeur que nous attribuons généralement à une variable ou que nous utilisons dans le cadre d'une expression. Par exemple :

e = exp(1.0)
height = radius * sin(radians)

Le premier exemple d'une fonction avec retour est area, qui retourne l'aire d'un cercle de rayon donné :

function area(radius)
    a = π * radius^2
    return a
end

Nous avons déjà vu la déclaration return. Cependant, dans une fonction avec retour, l'instruction return comprend une expression. Cette instruction signifie littéralement : « Quitter immédiatement la fonction et utiliser l'expression qui suit return comme valeur de retour ». L'expression peut être plus ou moins compliquée. Ainsi, la fonction area aurait pu être plus concise :

function area(radius)
    π * radius^2
end

En effet, la valeur retournée par une fonction est la valeur de la dernière expression évaluée qui, par défaut, est la dernière expression figurant dans le corps de la définition de la fonction.

Cependant, des variables temporaires comme a (deuxième cadre de cette section) et des déclarations de retour explicites facilitent grandement le débogage. Il est parfois même utile d'avoir plusieurs déclarations de retour, une dans chaque branche conditionnelle :

function absvalue(x)
    if x < 0
        return -x
    else
        return x
    end
end

Comme ces instructions return sont dans une branche conditionnelle alternative, une seule des options est empruntée. Dès qu'une déclaration return est exécutée, la fonction se termine sans exécuter d'instructions ultérieures. Le code qui apparaît après une instruction return ou après toute autre partie que le flux d'exécution ne peut jamais atteindre est appelé un code mort.

Dans une fonction avec retour, il est bon de s'assurer que tous les chemins possibles du programme aboutissent à une instruction return. Par exemple :

function absvalue(x)
    if x < 0
        return -x
    end
    if x > 0
        return x
    end
end

Cette fonction est incorrecte, car, si x vaut 0, aucune des deux conditions n'est avérée, si bien que la fonction se termine sans atteindre une instruction return. Si le flux d'exécution arrive ainsi à la fin d'une fonction, la valeur retournée est nothing, ce qui ne correspond pas à la valeur absolue de 0. Ceci est vérifiable :

julia> show(absvalue(0))
nothing

6-1-1. Exercice 6-1▲

À mesure que les fonctions deviennent de plus en plus volumineuses, le temps de débogage s'allonge. Pour faire face à des programmes de plus en plus complexes, il est astucieux de tirer parti d'un procédé appelé développement progressif ou incrémental. L'objectif est d'éviter de longues sessions de débogage en ajoutant et en testant individuellement un code de petite taille.

Par exemple, supposons que vous vouliez trouver la distance entre deux points, donnée par les coordonnées kitxmlcodeinlinelatexdvp(x_{1},y_{1})finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp(x_{2},y_{2})finkitxmlcodeinlinelatexdvp. Selon le théorème de Pythagore, la distance est donnée par :

La première étape consiste à examiner à quoi devrait ressembler une fonction distance en Julia. En d'autres termes, quelles sont les entrées (paramètres) et quelle est la sortie (valeur de retour) ?

Dans ce cas, les entrées sont deux points, que vous pouvez représenter à l'aide de quatre nombres. La valeur de retour est la distance représentée par une valeur en virgule flottante.

Dans l'immédiat, écrivons un aperçu de la fonction :

function distance(x₁, x₂, y₁, y₂)
    0.0
end

Évidemment, cette version ne calcule pas les distances ; elle retourne toujours zéro. Cependant, elle est syntaxiquement correcte. Elle fonctionne, ce qui signifie que vous pouvez la tester avant de la complexifier. Les numéros d'indice sont disponibles dans le codage des caractères Unicode (\_1 TAB, \_2 TAB, etc.).

Pour tester la nouvelle fonction, appelons-la avec des exemples d'arguments :

distance(1, 2, 4, 6)

Ces valeurs ont été choisies pour que la distance horizontale soit 3 et la distance verticale 4. De cette façon, le résultat est 5 : c'est-à-dire l'hypoténuse d'un triangle 3-4-5. Lorsqu'on teste une fonction, il est utile de connaître la bonne réponse.

À ce stade, il est acquis que la fonction est syntaxiquement correcte. Dès lors, du code peut être ajouté dans le corps. La prochaine étape raisonnable consiste à trouver les différences kitxmlcodeinlinelatexdvp(x_{2}-x_{1})finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp(y_{2}-y_{1})finkitxmlcodeinlinelatexdvp. La version suivante enregistre ces valeurs dans des variables temporaires et les affiche avec la macro @show.

function distance(x₁, x₂, y₁, y₂)
    dx = x₂ - x₁
    dy = y₂ - y₁
    @show dx  dy
    0.0
end

Pour un appel distance(1, 2, 4, 6), la fonction doit afficher dx = 3 et dy = 4. Si c'est le cas, cela signifie que la fonction reçoit les bons arguments et effectue correctement le premier calcul (sinon, il n'y a que quelques lignes à vérifier).

Ensuite, la somme des carrés de dx et dy peut être incorporée :

function distance(x₁, y₁, x₂, y₂)
    dx = x₂ - x₁
    dy = y₂ - y₁
    d² = dx^2 + dy^2
    @show d²
    0.0
end

Là encore, il convient de lancer le programme à ce stade et de vérifier le résultat (d² = 25). Les puissances sont également disponibles (\^2 TAB). Enfin, la fonction sqrt est introduite afin de calculer et de retourner le résultat :

function distance(x₁, y₁, x₂, y₂)
    dx = x₂ - x₁
    dy = y₂ - y₁
    d² = dx^2 + dy^2
    sqrt(d²)
end

Si tout fonctionne correctement, nous en avons terminé. Sinon, il sera nécessaire d'afficher la valeur de sqrt(d²) avant end à l'aide de @show.

La version finale de la fonction n'affiche rien lorsqu'elle est exécutée. Elle ne fait que retourner une valeur. Les instructions d'affichage que nous avons écrites sont utiles pour le débogage, mais, une fois la fonction opérationnelle, il convient de les supprimer. Un tel code est appelé « canevas » (ou scaffolding) parce qu'il est utile pour construire le programme tout en n'apparaissant pas dans le produit final.

Au début, il est judicieux de n'ajouter qu'une ou deux lignes de code à la fois. Avec une expérience s'affinant progressivement, il devient possible d'écrire et de déboguer des parties un peu plus longues. Quoi qu'il en soit, le développement incrémental permet de gagner beaucoup de temps de débogage.

Les principaux aspects du processus sont les suivants :

1. Commencer par un programme opérationnel et apporter de petites modifications progressives. À tout moment, s'il y a une erreur, il est essentiel d'avoir une bonne idée de l'endroit où elle se trouve ;
2. Utiliser des variables pour maintenir des valeurs intermédiaires afin de pouvoir les afficher et les vérifier ;
3. Une fois que le programme complété fonctionne, supprimer une partie du canevas ou consolider plusieurs instructions en expressions composées (voir la section 6.3Composition), mais à la condition que cela ne rende pas le programme difficile à lire.

6-2-1. Exercice 6-2▲

Bien entendu, une fonction peut être appelée depuis une autre. Par exemple, nous allons écrire une fonction qui prend deux points, le centre d'un cercle et un point sur la circonférence. Ceci nous permet de calculer le rayon et, partant, la surface de ce cercle.

Supposons que les coordonnées du centre soient enregistrées dans les variables kitxmlcodeinlinelatexdvpx_{c}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpy_{c}finkitxmlcodeinlinelatexdvp et que les coordonnées du point de la circonférence le soient dans kitxmlcodeinlinelatexdvpx_{p}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpy_{p}finkitxmlcodeinlinelatexdvp. La première étape consiste à trouver le rayon du cercle. Dans la section 6.2Développement progressif, nous avons écrit une fonction distance. En transposant pour le rayon :

radius = distance(xc, yc, xp, yp)

L'étape suivante consiste à trouver l'aire d'un cercle de ce rayon (ce que nous avons aussi écrit dans la section 6.1Valeurs retournées), ce qui fait que nous pouvons appeler cette fonction :

result = area(radius)

Par encapsulation, nous obtenons :

function circlearea(xc, yc, xp, yp)
    radius = distance(xc, yc, xp, yp)
    result = area(radius)
    return result
end

Les variables temporaires radius et result sont utiles pour le développement et le débogage. Lorsqu'il est opérationnel, le programme peut être rédigé de manière plus concise en composant les appels de fonction :

function circlearea(xc, yc, xp, yp)
    area(distance(xc, yc, xp, yp))
end

Les fonctions peuvent renvoyer des booléens, ce qui est souvent pratique pour cacher des tests complexes à l'intérieur de celles-ci. Par exemple :

function isdivisible(x, y)
    if x % y == 0
        return true
    else
        return false
    end
end

Il est courant de donner aux fonctions booléennes des noms qui ressemblent à des questions dichotomiques(8). La fonction isdivisible retourne soit true, soit false pour indiquer si x est divisible, ou non, par y.

Voici deux exemples :

julia> isdivisible(6, 3)
true
julia> isdivisible(6, 4)
false

Le résultat de l'opérateur == étant un booléen, la fonction peut être reformulée de manière plus concise :

function isdivisible(x, y)
    x % y == 0
end

Les fonctions booléennes sont souvent utilisées dans les déclarations conditionnelles :

if isdivisible(x, y)
    println("x est divisible par y")
end

Il pourrait être tentant d'écrire quelque chose comme ceci :

if isdivisible(x, y) == true
    println("x est divisible par y")
end

Cependant, la comparaison supplémentaire avec true est inutile.

6-4-1. Exercice 6-3▲

Nous n'avons couvert qu'un petit sous-ensemble de Julia. Cependant, Julia est un langage de programmation complet, ce qui signifie que tout ce qui est calculable peut être exprimé dans ce langage. Tout programme écrit à ce jour pourrait être retranscrit en utilisant uniquement les caractéristiques de Julia telles que présentées jusqu'à présent. En principe, il n'y a plus que quelques commandes à apprendre pour contrôler des périphériques comme la souris, les disques, etc.

Prouver cette affirmation est un exercice complexe réalisé pour la première fois par Alan Turing, un des pionniers de l'informatique(9) et mathématicien à l'origine. C'est pourquoi elle est connue sous le nom de thèse de Turing(10).

Pour se persuader de ce qui est réalisable avec les outils étudiés jusqu'à présent, nous allons évaluer quelques fonctions mathématiques définies de manière récursive. Une définition récursive est analogue à une définition circulaire, dans le sens où la définition contient une référence à ce qui y est défini (ou à son exact contraire). Une définition vraiment circulaire n'est pas très utile(11). Dans le dictionnaire anglais, voyons la définition de :

• vorpal an adjective used to describe something that is vorpal(12).

Nous pourrions imaginer en français :

• gauche inverse de la droite ;

• droite inverse de la gauche.

De telles définitions rendent perplexe. En revanche, si on cherche la définition de la fonction factorielle, désignée par le symbole !, on obtiendra probablement ceci :

Cette définition établit que la factorielle de 0 est 1 et que la factorielle de toute autre valeur n s'exprime comme n multiplié par la factorielle de n-1. Donc 3! est 3 fois 2!, avec 2! qui est 2 fois 1!, avec 1! qui est 1 fois 0!. En combinant le tout, 3! est égal à 3 * 2 * 1 * 1, ce qui fait 6.

Si un programmeur peut rédiger une définition récursive, il peut développer un programme Julia pour l'évaluer. La première étape consiste à décider des paramètres. Dans ce cas, il doit être clair que la fonction factorielle prend un entier :

function fact(n)
end

S'il advenait que l'argument vaille 0, la fonction devrait retourner 1 :

function fact(n)
    if n == 0
        return 1
    end
end

Sinon — et c'est la partie intéressante —, nous devons faire un appel récursif pour trouver la factorielle de n-1 et ensuite la multiplier par n :

function fact(n)
    if n == 0
        return 1
    else
        recurse = fact(n-1)
        result = n * recurse
        return result
    end
end

Le flux d'exécution de ce programme est similaire au flux de countdown vu dans la section 5.8Récursion. Si nous appelons fact avec n = 3 :

• Vu que 3 n'est pas égal à 0, nous prenons la deuxième branche et calculons la factorielle de n-1…

  • Puisque 2 n'est pas égal à 0, nous prenons la deuxième branche et calculons la factorielle de n-1…

    • Puisque 1 n'est pas égal à 0, nous prenons la deuxième branche et calculons la factorielle de n-1…

      • Puisque nous arrivons au cas 0, nous prenons la première branche et nous retournons 1 sans faire d'appels récursifs supplémentaires.
    • La valeur de retour, 1, est multipliée par n, qui est 1, et le résultat est retourné.
  • La valeur de retour, 1, est multipliée par n, qui vaut 2, et le résultat est retourné.
• La valeur de retour 2 est multipliée par n (qui vaut 3) et le résultat, c'est-à-dire 6, devient la valeur de retour de l'appel de fonction qui a lancé l'ensemble du processus.

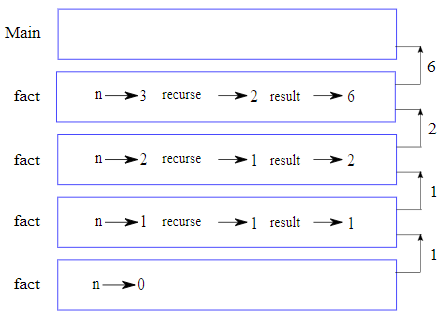
Le diagramme de pile (figure 6.5.1) illustre cette séquence d'appels de fonction. Les valeurs de retour sont indiquées en remontant dans la pile. Dans chaque cadre, la valeur de retour est celle de result, qui est le produit de n et de recurse. Dans le dernier cadre, les variables locales recurse et result n'existent pas, car la branche qui les crée n'est pas exécutée.

Suivre le déroulement de l'exécution est une manière de lire les programmes, bien que cela puisse s'avérer ardu. Souvent, nous agissons en confiance. Ainsi, lorsque nous arrivons à un appel de fonction, au lieu de suivre le flux d'exécution, nous supposons que la fonction se comporte correctement et retourne le bon résultat.

En fait, ceci est déjà vrai, par exemple, lorsque des fonctions internes sont utilisées. Lorsque cos() ou exp() sont appelées, leur utilisateur n'examine pas le corps de ces fonctions. Il suppose assez naturellement qu'elles sont opérationnelles, parce que les personnes qui les ont écrites sont de bons programmeurs.

Il en va de même lorsque nous appelons une de nos propres fonctions. Par exemple, dans les fonctions booléennes (section 6.4Fonctions booléennes), nous avons écrit isdivisible qui détermine si un nombre est divisible par un autre. Une fois que nous nous sommes convaincus que cette fonction est correcte — en examinant le code et en faisant des tests, nous pouvons utiliser la fonction sans devoir analyser à nouveau le corps.

Il en va de même pour les programmes récursifs. Arrivé à un appel récursif, au lieu de suivre le déroulement de l'exécution, il est supposé que l'appel récursif fonctionne (c'est-à-dire qu'il retourne le résultat correct). Ensuite, survient la question : « En supposant que je puisse trouver la factorielle de kitxmlcodeinlinelatexdvpn-1finkitxmlcodeinlinelatexdvp, puis-je calculer la factorielle de kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp ? ». Il est clair que cela peut se faire en multipliant par n.

Il est un peu étrange d'accepter que la fonction se comporte correctement alors même qu'on n'a pas fini de l'écrire. C'est pour cela que l'expression « acte de confiance » peut être invoquée.

Après la factorielle, l'exemple le plus courant d'une fonction mathématique définie de manière récursive est la suite de Fibonacci.

Voici un programme Julia représentant cette suite :

function fib(n)
    if n == 0
        return 0
    elseif n == 1
        return 1
    else
        return fib(n-1) + fib(n-2)
    end
end

Suivre le déroulement de l'exécution, même pour des valeurs assez faibles de n, conduit rapidement à la saturation. Néanmoins, selon le principe de l'acte de confiance, il suffit de constater que deux appels récursifs fonctionnent correctement, pour admettre que le bon résultat est obtenu par addition.

Que se passe-t-il si fact est appelée avec 1.5 comme argument ?

julia> fact(1.5)
ERROR: UndefVarError: fact not defined
Stacktrace:
  [1] fact(::Float64) at ./REPL[3]:2

Cela ressemble à une récursion infinie. Au premier abord, c'est surprenant, car la fonction possède un cas de base lorsque n == 0. Cependant, si n n'est pas un entier, le cas de base peut ne pas être atteint. En conséquence, la récursion opère à l'infini.

Dans le premier appel récursif, la valeur de n est 0.5. Dans le suivant, elle est -0.5. À partir de là, cette valeur devient inférieure à 0 sans jamais passer par 0.

Pour résorber ce problème, nous avons deux options : (i) soit essayer de généraliser la fonction factorielle pour travailler avec des nombres à virgule flottante, (ii) soit faire vérifier le type de son argument à la fonction fact. La première option recourt à la fonction gamma, mais cela dépasse le cadre de ce livre. La seconde option est à notre portée.

L'opérateur interne isa permet de vérifier le type de l'argument. Par ailleurs, pourquoi ne pas s'assurer que l'argument est positif ?

function fact(n)
    if !(n isa Int64) 
        error("La factorielle est seulement définie pour les entiers.")
    elseif n < 0
        error("La factorielle n'est pas définie pour les entiers négatifs.")
    elseif n == 0
        return 1
    else
        return n * fact(n-1)
    end
end

Le premier cas de base traite des non-entiers, le second des entiers négatifs. Dans les deux cas, le programme affiche un message d'erreur et ne retourne rien pour indiquer que quelque chose s'est mal passé :

julia> fact("Knuth")
ERROR: La factorielle est seulement définie pour les entiers.
julia> fact(-2)
ERROR: La factorielle n'est pas définie pour les entiers négatifs.

Si les deux contrôles sont correctement franchis, cela signifie que n est positif ou nul. En conséquence, la preuve est faite que la récursion prend fin.

Ce programme démontre un schéma parfois appelé « sentinelle ». Les deux premières conditions agissent comme des sentinelles, protégeant le code qui suit des valeurs qui pourraient causer une erreur. Les sentinelles permettent de prouver l'exactitude du code.

Dans la section 14.5Levée des exceptions, nous verrons une option plus souple à l'affichage d'un message d'erreur : la levée d'une exception.

La subdivision d'un programme de grande taille en petites fonctions crée des points de contrôle naturels pour le débogage. Si une fonction n'opère pas correctement, trois possibilités sont à envisager :

1. Un problème avec les arguments que la fonction reçoit : une condition a priori est violée ;

2. Un problème avec la fonction elle-même : une condition a posteriori est violée ;

3. Un problème avec la valeur de retour ou la façon dont elle est utilisée.

Pour écarter la première possibilité, il convient d'ajouter une instruction d'affichage au début de la fonction et d'y indiquer les valeurs des paramètres (et peut-être leur type). Une option consiste à écrire un code qui vérifie explicitement les conditions préalables.

Si les paramètres semblent bons, il convient d'ajouter une instruction d'affichage avant chaque instruction de retour et afficher la valeur de retour. Lorsque c'est possible, il est conseillé de vérifier le résultat à la main. Exécuter des appels de la fonction avec des valeurs qui facilitent la vérification du résultat aide beaucoup au débogage (voir la section 6.2Développement progressif qui traite du développement incrémental).

Si la fonction semble opérationnelle, l'appel de la fonction doit être examiné pour s'assurer que la valeur de retour est utilisée correctement.

L'ajout d'instructions d'affichage au début et à la fin d'une fonction peut contribuer à rendre le flux d'exécution plus compréhensible. Par exemple, voici une version de fact avec des instructions d'affichage :

function fact(n)
    space = " " ^ (4 * n)
    println(space, "factorial ", n)
    if n == 0
        println(space, "returning 1")
        return 1
    else
        recurse = fact(n-1)
        result = n * recurse
        println(space, "returning ", result)
        return result
    end
end

space est une chaîne de caractères d'espacement qui contrôle l'indentation de la sortie :

julia> fact(4)
                factorial 4
            factorial 3
        factorial 2
    factorial 1
factorial 0
returning 1
    returning 1
        returning 2
            returning 6
                returning 24
24

Ce type de résultat peut être utile quand l'exécution d'un programme se passe de manière déroutante. Mettre au point un canevas efficace prend du temps, mais cette technique en épargnera beaucoup lors du débogage.

variable temporaire variable utilisée pour stocker une valeur intermédiaire dans un calcul complexe.

code mort partie d'un programme qui ne peut jamais fonctionner, souvent parce qu'il apparaît après une instruction de retour.

développement progressif (ou incrémental) plan de développement de programmes destiné à limiter le débogage en ajoutant et en testant seulement de petits blocs d'instructions, un à un.

canevas (scaffolding) code utilisé pendant le développement du programme, mais qui ne fait pas partie de la version finale.

sentinelle modèle de programmation qui utilise une déclaration conditionnelle pour vérifier et gérer les circonstances susceptible de causer une erreur.

6-11-1. Exercice 6-4▲

function b(z)
    prod = a(z, z)
    println(z, " ", prod)
    prod
end

function a(x, y)
    x = x + 1
    x * y
end

function c(x, y, z)
    total = x + y + z
    square = b(total)^2
    square
end

x = 1
y = x + 1
println(c(x, y+3, x+y))

6-11-2. Exercice 6-5▲

6-11-3. Exercice 6-6▲

function first(word)
    first = firstindex(word)
    word[first]
end

function last(word)
    last = lastindex(word)
    word[last]
end

function middle(word)
    first = firstindex(word)
    last = lastindex(word)
    word[nextind(word, first) : prevind(word, last)]
end

6-11-4. Exercice 6-7▲

6-11-5. Exercice 6-8▲