5. Conditions et récursion▲
Le sujet principal de ce chapitre est la déclaration if, qui exécute un code différent selon l'état du programme. Auparavant, considérons deux nouveaux opérateurs : la division euclidienne ÷ (\div TAB)(7) et le modulo.
5-1. Division euclidienne (entière) et modulo▲
L'opérateur de division euclidienne ou entière ÷ divise deux nombres et arrondit au quotient, c'est-à-dire au nombre entier inférieur. Par exemple, supposons que la durée d'un film soit de 105 minutes. Combien de temps en heures cela représente-t-il ? La division conventionnelle / donne un nombre à virgule flottante :
2.
3.
4.
julia> minutes = 105
105
julia> minutes / 60
1.75
Or, nous n'écrivons normalement pas les heures avec des points décimaux. La division entière ÷ retourne le quotient :
2.
julia> heures = minutes ÷ 60
1
Pour obtenir le reste, nous pourrions pratiquer ainsi :
2.
julia> reste = minutes - heures * 60
45
Une autre solution consiste à utiliser l'opérateur modulo, %, qui divise deux nombres et retourne le reste.
2.
julia> reste = minutes % 60
45
L'opérateur modulo est plus utile qu'il n'y paraît, par exemple, dans le cas où il faut déterminer si un nombre est divisible par un autre. Si x % y vaut zéro, alors x est divisible par y. L'opérateur modulo est commode pour extraire le ou les chiffres les plus à droite d'un nombre. Par exemple, en base 10, x % 10 donne le chiffre le plus à droite d'un nombre entier x. De même, x % 100 donne les deux derniers chiffres.
5-2. Expressions booléennes▲
Une expression booléenne est une expression qui est soit vraie, soit fausse. Les exemples suivants utilisent l'opérateur ==, qui compare deux opérandes et retourne true s'ils sont égaux et false sinon :
2.
3.
4.
julia> 5 == 5
true
julia> 5 == 6
false
true et false sont des valeurs spéciales qui appartiennent au type Bool. Il ne s'agit en rien de chaînes de caractères :
2.
3.
4.
julia> typeof(true)
Bool
julia> typeof(false)
Bool
L'opérateur == fait partie des opérateurs relationnels (voir tableau 5.1).
Bien que ces opérations soient probablement familières, les symboles de Julia sont différents des symboles mathématiques. Une erreur courante consiste à utiliser un signe égal simple (=) au lieu d'un signe égal double (==). Il faut garder à l'esprit que = est un opérateur d'affectation et que == est un opérateur relationnel. Il n'existe pas de =< ou de =>.
|
Opérateurs |
Signification |
|---|---|
|
x == y |
# x est égal à y |
|
# x n'est pas égal à y |
|
|
# x est plus grand que y |
|
|
# x est plus petit que y |
|
|
# x est plus grand ou égal à y |
|
|
# x est plus petit ou égal à y |
|
5-3. Opérateurs logiques▲
Il y a trois opérateurs logiques : && (et), || (ou) et ! (non). La signification de ces opérateurs est la même que dans le langage courant. Par exemple, x > 0 && x < 10 n'est vrai que si x appartient au segment fermé [1,9].
L'expression n % 2 == 0 || n % 3 == 0 est vraie si l'une ou l'autre des conditions (ou les deux) est vraie, c'est-à-dire si le nombre est divisible par 2 ou par 3.
Les deux && et || s'associent à droite, mais && a une priorité plus élevée que ||.
Enfin, l'opérateur ! annule une expression booléenne, donc !(x > y) est vrai si x > y est faux, c'est-à-dire si x est inférieur ou égal à y.
5-4. Exécution conditionnelle▲
Afin d'écrire des programmes utiles, il est presque toujours nécessaire de pouvoir vérifier les conditions et modifier le comportement du programme en conséquence. Les déclarations conditionnelles nous offrent cette capacité. La forme la plus simple est la déclaration if :
2.
3.
if x > 0
println("x est positif")
end
L'expression booléenne après if est appelée une condition. Si elle est vraie, les instructions du bloc indenté sont exécutées. Sinon, rien ne se passe.
Les instructions if ont la même structure que les définitions de fonctions : un en-tête suivi d'un corps terminé par le mot-clé end. Les instructions de ce type sont dites composées.
Il n'y a pas de limite au nombre d'instructions formant le corps. Parfois, il est utile d'avoir un corps sans déclaration (généralement pour réserver la place pour un code non encore écrit).
2.
3.
if x < 0
# À FAIRE gérer les valeurs négatives!
end
5-5. Exécution alternative▲
Une deuxième forme de la déclaration if consiste en une « exécution alternative » avec deux possibilités. La condition détermine quelle branche de l'alternative doit être exécutée. La syntaxe est :
2.
3.
4.
5.
if x % 2 == 0
println("x est pair")
else
println("x est impair")
end
Lorsque x est divisible par 2, le programme affiche x est pair. Si la condition est fausse, la deuxième série d'instructions est exécutée. Comme la condition doit être vraie ou fausse, l'une des branches de l'alternative est toujours exécutée.
5-6. Enchaînement de conditions▲
Il arrive souvent qu'un programme requière plus de deux branches. Une manière de procéder consiste à exploiter les enchaînements de conditions avec le mot-clé elseif :
2.
3.
4.
5.
6.
7.
if x < y
println("x est inférieur à y")
elseif x > y
println("x est supérieur à y")
else
println("x est égal à y")
end
À nouveau, seule une branche fonctionnera. Il n'y a pas de limite au nombre de déclarations elseif. S'il y a une clause else, elle doit se trouver à la fin, mais n'est pas nécessaire.
2.
3.
4.
5.
6.
7.
if choice == "a"
draw_a
elseif choice == "b"
draw_b
elseif choice == "c"
draw_c
end
Chaque condition est examinée dans l'ordre. Si la première est fausse, la suivante est vérifiée et ainsi de suite. Si l'une d'entre elles est vraie, la branche correspondante est parcourue et la déclaration se termine. Même si plus d'une condition est vraie, seule la première branche vraie est exécutée.
5-7. Imbrication de conditions▲
Une condition peut être imbriquée dans une autre. L'exemple de la section précédente peut s'écrire ainsi :
2.
3.
4.
5.
6.
7.
8.
9.
if x == y
println("x est égal à y")
else
if x < y
println("x est inférieur à y")
else
println("x est égal à y")
end
end
La condition « extérieure » contient deux branches. La première branche contient une seule instruction. La deuxième branche renferme un autre bloc if, qui lui-même comprend deux branches. Ces deux branches contiennent des instructions simples, bien qu'elles puissent également être des instructions conditionnelles à leur tour.
Même lorsque l'indentation est scrupuleusement observée, les conditions imbriquées deviennent très rapidement difficiles à lire. Il est bon de les éviter quand c'est possible.
Les opérateurs logiques permettent souvent de simplifier les déclarations conditionnelles imbriquées. Par exemple, le code suivant peut être reformulé en utilisant une seule condition :
2.
3.
4.
5.
if 0 < x
if x < 10
println("x est un nombre positif")
end
end
L'instruction d'affichage ne fonctionne que si les deux conditions sont passées. Le même résultat peut être obtenu avec l'opérateur && :
2.
3.
if 0 < x && x < 10
println("x est un nombre positif")
end
5-8. Récursion▲
Il est permis qu'une fonction en appelle une autre et aussi qu'elle s'appelle elle-même. C'est un des aspects les plus « magiques » de la programmation. Considérons, par exemple, la fonction suivante :
2.
3.
4.
5.
6.
7.
8.
function countdown(n)
if n ≤ 0
println("mise à feu !")
else
print(n, " ")
countdown(n-1)
end
end
Si n vaut 0 ou est négatif, le programme affiche "mise à feu !". Sinon, il affiche n suivi d'un espace. Ensuite, le programme appelle une fonction appelée countdown (compte à rebours) se passant à elle même n-1 comme argument.
Que se passe-t-il si nous appelons cette fonction comme ceci ?
2.
julia> countdown(3)
3 2 1 "mise à feu!"
L'exécution de countdown commence avec n = 3 et, comme n est supérieur à 0, le programme passe à l'intérieur du else et affiche la valeur 3 suivie d'un espace. L'exécution de la fonction countdown s'appelle elle-même et se poursuit avec n = 2. Puisque n est supérieur à 0, le programme passe à nouveau dans la partie else ; il affiche la valeur 2 suivie d'un espace. Le programme continue avec un autoappel de countdown avec n = 1. Puisque n est supérieur à 0, le programme passe à nouveau dans la partie else ; il affiche la valeur 1 suivie d'un espace. Le cycle se prolonge avec un autoappel de countdown qui se poursuit avec n = 0. Cette fois, comme n n'est pas supérieur à 0, le programme affiche l'expression "mise à feu !".
Une fonction qui s'appelle elle-même est récursive ; le processus qui y est associé se nomme une récursion.
Voici un autre exemple d'une fonction qui affiche n fois une chaîne de caractères à l'écran :
2.
3.
4.
5.
6.
7.
function printn(s, n)
if n ≤ 0
return
end
println(s)
printn(s, n-1)
end
Si n ≤ 0, la déclaration return permet de quitter la fonction. Le flux d'exécution revient immédiatement à l'instruction appelante. Donc, le programme s'arrête et les autres lignes de la fonction ne sont pas exécutées. Par exemple, imaginons la fonction appelante suivante :
2.
3.
printn("bonjour", 2)
bonjour
bonjour
Du fait que n = 2, le programme affiche une première fois bonjour. Puis, il appelle printn avec n = 1. Cet autoappel correspond à printn("bonjour", 1). Le programme affiche une fois encore bonjour. Puis, il appelle printn avec n = 0. En rentrant une troisième fois dans la fonction, le programme constate que la condition n ≤ 0 est remplie : il effectue un return.
Pour des exemples simples comme celui-ci, il est probablement plus facile d'utiliser une boucle for. Cependant, nous verrons plus tard des exemples difficiles à écrire avec une boucle for et beaucoup plus faciles à rédiger en invoquant une récursion.
5-9. Diagrammes de pile pour les fonctions récursives▲
Dans la section 3.9Diagrammes de pile, nous avons utilisé un diagramme de pile pour représenter l'état d'un programme lors d'un appel de fonction. Le même type de diagramme peut aider à interpréter une fonction récursive.
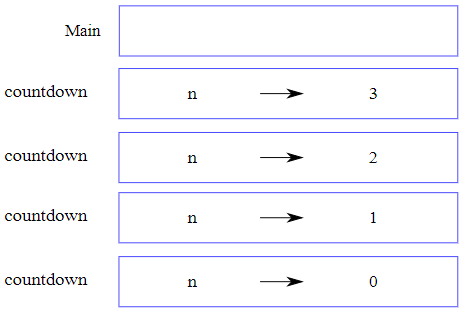
Chaque fois qu'une fonction est appelée, Julia crée un cadre pour contenir les variables et paramètres locaux de la fonction. Pour une fonction récursive, il peut y avoir plus d'un cadre sur la pile en même temps. La figure 5.9.1 montre un diagramme de pile pour la fonction countdown (compte à rebours) appelée avec n = 3.
|
|
Comme d'habitude, le haut de la pile est le cadre de Main. Il est vide parce qu'aucune variable n'a été instanciée dans Main et qu'aucun argument ne lui a été passé. Les quatre cadres de countdown ont des valeurs différentes pour le paramètre n. Le bas de la pile, où n = 0, est appelé le cas de base. Aucun appel récursif n'a lieu pour n = 0, il n'y a donc plus de cadres en dessous.
5-9-1. Exercice 5-1▲
En guise d'exercice, dessinez un diagramme de pile pour une fonction printn appelée avec s = "bonjour" et n = 2. Ensuite, écrivez une fonction appelée do_n qui prend un objet de fonction et un nombre n comme argument, et qui appelle la fonction n fois.
5-10. Récursion infinie▲
Si une récursion n'atteint jamais le cas de base, elle continue à faire des appels récursifs indéfiniment : le programme ne se termine jamais. Il s'agit là d'une récursion infinie, ce qui constitue un mauvais cas de figure. Voici un programme minimal avec une récursion infinie :
2.
3.
function recurse()
recurse()
end
Dans la plupart des environnements de programmation, un programme à récursion infinie ne fonctionne pas indéfiniment. Julia envoie un message d'erreur lorsque la profondeur de récursion maximale est atteinte :
2.
3.
4.
julia> recurse()
ERROR: StackOverflowError:
Stacktrace:
[1] recurse() at ./REPL[1]:2 (repeats 80000 times)
La trace d'appels (appelée encore trace de pile ou stacktrace) est un peu plus grande que celle que nous avons vue dans le chapitre 3Fonctions. Lorsque l'erreur se produit, il y a 80 000 images récurrentes dans la pile.
Lorsqu'une récursion infinie est rencontrée accidentellement, la fonction incriminée doit être analysée pour confirmer qu'un cas de base ne fait pas d'appel récursif. Si un cas de base existe, il est nécessaire de vérifier que son accès est garanti.
5-11. Saisie au clavier▲
Les programmes que nous avons écrits jusqu'ici n'acceptent aucune entrée de la part de l'utilisateur. Leur exécution produit toujours le même résultat.
Julia fournit une fonction interne appelée readline qui arrête le programme et attend que l'utilisateur saisisse une information. Lorsque l'utilisateur presse la touche ENTER, le programme reprend et readline transmet l'information que l'utilisateur a saisie sous forme de chaîne de caractères.
2.
3.
julia> texte = readline()
Qu'attendez-vous?
"Qu'attendez-vous?"
Avant d'obtenir la contribution de l'utilisateur, il est conseillé d'afficher un message lui indiquant ce qu'il doit saisir :
2.
3.
julia> print("Quel est votre prénom? "); readline()
Quel est votre prénom? Thierry
"Thierry"
Un point-virgule ; permet de placer plusieurs déclarations sur la même ligne. Dans le REPL, seul le dernier énoncé retourne sa valeur.
S'il est attendu de l'utilisateur qu'il saisisse un entier, il convient de convertir la valeur transmise en Int64 :
2.
3.
4.
5.
julia> print("Quelle est la célérité du son dans l'air au niveau de la mer (m/s)?"); c = readline()
Quelle est la célérité du son dans l'air au niveau de la mer (m/s)? 340
"340"
julia> parse(Int64, c)
340
Toutefois, si l'utilisateur saisit autre chose qu'une suite de chiffres, une erreur apparaît à la conversion :
2.
3.
4.
5.
6.
julia> print("Quelle est la célérité du son dans l'air au niveau de la mer (m/s)?"); c = readline()
Quelle est la célérité du son dans l'air au niveau de la mer (m/s)? Que signifie célérité?
"Que signifie célérité?"
julia> parse(Int64, c)
ERROR: ArgumentError invalid base 10 digit 'C' in "Célérité?"
[…]
Ultérieurement, nous verrons comment gérer ce genre d'erreur.
5-12. Débogage▲
Lorsqu'une erreur de syntaxe ou d'exécution se produit, le message d'erreur contient beaucoup d'informations, mais il peut être surchargé. Les parties les plus utiles sont généralement :
- quel type d'erreur s'est-il produit ?
- à quel endroit du programme l'erreur s'est-elle produite ?
Les erreurs de syntaxe sont généralement faciles à trouver, mais quelques astuces existent. En général, les messages d'erreur indiquent l'endroit où le problème a été découvert, mais l'erreur réelle peut se situer en amont dans le code, parfois sur la ligne précédente.
Il en va de même pour les erreurs d'exécution. Supposons que nous tentions de calculer un rapport signal/bruit en décibels (Signal-to-Noise Ratio, SNR). La formule est la suivante :
kitxmlcodelatexdvpSNR_{\mathrm{dB}}=10\log10\left(\frac{P_{signal}}{P_{bruit}}\right)finkitxmlcodelatexdvpoù kitxmlcodeinlinelatexdvpPfinkitxmlcodeinlinelatexdvp représente l'amplitude. En Julia, il est possible d'écrire ce code :
2.
3.
4.
5.
signal_power = 9
noise_power = 10
ratio = signal_power ÷ noise_power
decibels = 10 * log10(ratio)
print(decibels)
Cependant, Julia retourne :
-Inf
Ce n'est pas le résultat attendu. Pour trouver l'erreur, il pourrait être utile d'afficher la valeur de ratio, qui s'avère valoir 0. Le problème se situe à la ligne 3, qui utilise la division euclidienne ÷ au lieu de la division décimale (/).
Il est nécessaire de prendre le temps de lire attentivement les messages d'erreur, bien qu'ils ne soient pas forcément explicites.
5-13. Glossaire▲
division euclidienne opération, notée ÷, qui divise deux nombres et les arrondit au nombre entier inférieur (à la différence de la division décimale, qui retourne un quotient à virgule flottante).
opérateur modulo opérateur, désigné par le signe pourcentage (%), qui fonctionne sur des nombres entiers et retourne le reste lorsqu'un nombre est divisé par un autre.
expression booléenne expression dont la valeur est soit vraie (true), soit fausse (false).
opérateur relationnel un des opérateurs qui comparent deux opérandes : ==, ≠ (!=), >, <, ≥ (>=) et ≤ (<=).
opérateur logique un des opérateurs qui combinent les expressions booléennes : && (et), || (ou) et ! (non).
déclaration conditionnelle déclaration qui contrôle le flux d'exécution en fonction de certaines conditions.
condition expression booléenne dans une déclaration conditionnelle qui détermine quelle branche emprunter.
instruction composée instruction complexe qui se compose d'un en-tête et d'un corps. Le corps est terminé par le mot-clé end.
branche une des options d'instructions dans une déclaration conditionnelle.
chaîne conditionnelle déclaration conditionnelle avec une série de branches alternatives.
imbrication conditionnelle déclaration conditionnelle qui apparaît dans une des branches d'une autre déclaration conditionnelle.
instruction de retour instruction qui fait qu'une fonction s'arrête immédiatement et revient à l'appelant.
récursion processus d'autoappel d'une fonction en cours d'exécution.
cas de base branche conditionnelle dans une fonction récursive qui n'effectue pas d'appel récursif.
récursion infinie récursion qui n'a pas de cas de base ou qui ne l'atteint jamais. Finalement, une récursion infinie provoque une erreur d'exécution.
5-14. Exercices▲
5-14-1. Exercice 5-2▲
La fonction time retourne le temps actualisé, au méridien de Greenwich en secondes depuis une date de référence arbitraire qui, sur les systèmes kitxmlcodeinlinelatexdvp{\rm\small UNIX}finkitxmlcodeinlinelatexdvp, est le 1er janvier 1970.
2.
julia> time()
1.602969109299345e9
Écrivez un script qui lit l'heure actuelle puis la convertit en jours, heures, minutes et secondes depuis la date de référence.
5-14-2. Exercice 5-3▲
Selon le dernier théorème de Fermat, il n'existe pas d'entiers positifs kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpcfinkitxmlcodeinlinelatexdvp tel que pour toute valeur de kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp > 2 :
kitxmlcodelatexdvpa^{n}+b^{n}=c^{n}finkitxmlcodelatexdvp-
Écrivez une fonction appelée checkfermat qui prend quatre paramètres (kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpcfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp) et qui vérifie si le théorème de Fermat est valide. Si n est supérieur à 2 et que a
^n+b^n==c^n, le programme doit afficher « Diantre, Fermat avait tort ! ». Sinon, le programme doit afficher « Non, ça ne fonctionne pas… ». - Écrivez une fonction qui invite l'utilisateur à entrer des valeurs pour a, b, c et n, les convertit en nombres entiers et utilise checkfermat pour vérifier s'ils violent le théorème de Fermat.
5-14-3. Exercice 5-4▲
Avec trois bâtonnets, vous pouvez éventuellement construire un triangle. Par exemple, si l'un des bâtonnets mesure 12 cm de long et les deux autres 1 cm de long, vous ne pourrez pas faire se rencontrer les bâtonnets courts. Pour trois longueurs quelconques, il existe un test simple permettant de déterminer s'il est possible de former un triangle :
Si une des trois longueurs est supérieure à la somme des deux autres, un triangle sera impossible à former. Par ailleurs, si la somme de deux longueurs est égale à la troisième, nous obtenons un triangle dégénéré.
-
Écrivez une fonction appelée istriangle qui prend trois entiers comme arguments et qui imprime soit « Oui » soit « Non », selon que vous pouvez ou non former un triangle à partir de bâtonnets ayant les longueurs entrées.
- Écrivez une fonction qui invite l'utilisateur à entrer trois longueurs de bâtonnets, les convertit en nombres entiers et utilise istriangle pour vérifier si les bâtonnets ayant les longueurs données peuvent former un triangle.
5-14-4. Exercice 5-5▲
Quel est le résultat du programme suivant ? Dessinez un diagramme de pile qui montre l'état du programme lorsqu'il affiche le résultat.
2.
3.
4.
5.
6.
7.
8.
9.
function recurse(n, s)
if n == 0
println(s)
else
recurse(n-1, n+s)
end
end
recurse(3, 0)
Que se passerait-il si l'appel de fonction devenait : recurse(-1, 0) ?
Écrivez une chaîne de caractères qui explique tout ce que quelqu'un doit savoir pour utiliser cette fonction (et rien d'autre).
Les exercices suivants utilisent le module ThinkJulia, décrit dans le chapitre 4Étude de cas : Conception d'une interface.
5-14-5. Exercice 5-6▲
Lisez la fonction suivante. Pouvez-vous déterminer ce qu'elle effectue (voir les exemples dans le chapitre 4Étude de cas : Conception d'une interface) ? Ensuite, exécutez-la pour voir si vous avez bien compris.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
function draw(t, length, n)
if n == 0
return
end
angle = 50
forward(t, length*n)
turn(t, -angle)
draw(t, length, n-1)
turn(t, 2*angle)
draw(t, length, n-1)
turn(t, -angle)
forward(t, -length*n)
end