Think Julia

Un module est un fichier qui contient un ensemble de fonctions connexes. Julia fournit certains modules dans sa bibliothèque standard. Des fonctionnalités supplémentaires peuvent être ajoutées à partir d'une collection croissante de paquets. Le lecteur se référera à Julia Observer.

Les paquets peuvent être installés à partir du REPL en entrant dans le mode Pkg du REPL à l'aide de la touche ].

(@v1.5) pkg> add https://github.com/BenLauwens/ThinkJulia.jl

L'installation peut prendre du temps.

Avant de pouvoir utiliser les fonctions d'un module, nous devons importer ce dernier avec une déclaration d'utilisation :

using ThinkJulia

🐢 = Turtle()
Turtle(0.0, 0.0, true, 0.0, (0.0, 0.0, 0.0))

Le module ThinkJulia fournit une fonction appelée Turtle qui crée un objet nommé Luxor.Turtle, que nous attribuons à une variable nommée 🐢 (:turtle: TAB). Une fois que nous avons créé une tortue, nous pouvons appeler une fonction pour la déplacer sur une feuille dessin. Par exemple, ce code fait avancer la tortue :

@svg begin
    forward(🐢, 100)
end
width: 600.0 
height: 600.0 
filename: luxor-drawing-165611_608.svg 
type: svg

En conséquence de quoi, un graphique — intitulé, en l'occurrence, luxor-drawing-165611_608.svg — s'affiche dans la partie Plots du REPL. Nous pouvons effectuer une recherche pour déterminer dans quel répertoire se trouve ce fichier (sous GNU/Linux : sudo updatedb et, ensuite en mode utilisateur, locate indiquera l'emplacement du fichier .svg). Le résultat devrait ressembler au dessin de la figure 4.1.1.

Le mot-clé @svg permet à une macro de fonctionner, qui dessine une image SVG. Les macros sont une fonctionnalité importante, mais avancée de Julia. Les arguments de marche sont 🐢 et une distance exprimées en pixels. De ce fait, la taille réelle dépend de l'affichage de l'utilisateur.

turn est une autre fonction pouvant être sollicitée avec 🐢 comme premier argument et qui permet de réorienter la tortue. Le deuxième argument que prend turn est un angle exprimé en degrés.

De plus, chaque tortue tient un stylo, qui est soit vers le bas, soit vers le haut. Si le stylo est vers le bas, la tortue laisse une trace lorsqu'elle se déplace. A contrario, si le stylo est relevé, la tortue peut avancer, mais sans déposer de trace. Les fonctions penup et pendown signifient respectivement stylo baissé et stylo relevé.

Pour dessiner un angle droit, modifions l'appel de la macro :

@svg begin
    forward(🐢, 100)
    turn(🐢, -90)
    forward(🐢, 100)
end

Nous devrions observer un dessin tel que représenté dans la figure 4.1.2.

4-1-1. Exercice 4-1▲

Il y a beaucoup de chances que vous ayez écrit ceci :

@svg begin
    forward(🐢, 100)
    turn(🐢, -90)
    forward(🐢, 100)
    turn(🐢, -90)
    forward(🐢, 100)
    turn(🐢, -90)
    forward(🐢, 100)
end

Nous pouvons faire la même chose de manière plus concise avec une déclaration for :

julia> for i in 1:4
             println("Hello!")
       end
Hello!
Hello!
Hello!
Hello!

C'est l'utilisation la plus simple de la déclaration for. Nous en verrons davantage plus tard. Cependant, cela devrait suffire pour reformuler le programme de dessin de carré. Ne continuez pas tant que vous n'aurez pas réussi.

Voici une déclaration for qui dessine un carré :

🐢 = Turtle()
@svg begin
    for i in 1:4
        forward(🐢, 100)
        turn(🐢, -90)
    end
end

La syntaxe d'une déclaration for est similaire à celle d'une définition de fonction. Elle comporte un en-tête et un corps qui se termine par le mot-clé end. Le corps peut contenir un nombre quelconque d'instructions. Une instruction for est également appelée boucle, car le flux d'exécution passe par le corps et revient ensuite en boucle vers le haut. Dans le cas présent, le corps est exécuté quatre fois.

Cette version est en fait un peu différente du précédent code de dessin de carré parce qu'elle effectue une rotation supplémentaire après avoir dessiné le dernier côté du carré. Cette rotation supplémentaire allonge le temps d'exécution, mais elle simplifie le code, parce que le programme exécute la même chose dans chaque boucle. Cette version a également pour effet de laisser la tortue dans la position de départ, tournée dans la direction initiale.

Voici une série d'exercices utilisant Turtle. Ils sont censés être amusants, mais ils ont aussi un but. Pendant que vous travaillez sur ces exercices, réfléchissez à l'intérêt qu'ils présentent.

4-3-1. Exercice 4-2▲

4-3-2. Exercice 4-3▲

4-3-3. Exercice 4-4▲

4-3-4. Exercice 4-5▲

4-3-5. Exercice 4-6▲

4-3-6. Exercice 4-7▲

Le premier exercice demande de placer le code de dessin square dans une définition de fonction et d'appeler la fonction en passant la tortue comme paramètre. Voici une solution :

function square(t)
    for i in 1:4
        forward(t, 100)
        turn(t, -90)
    end
end

🐢 = Turtle()
@svg begin
    square(🐢)
end

Les déclarations forward et turn sont indentées deux fois pour montrer qu'elles se trouvent à l'intérieur de la boucle for figurant elle-même à l'intérieur de la définition de la fonction square.

À l'intérieur de la fonction square, t fait référence à la tortue 🐢, turn(t, -90) a donc le même effet que turn(🐢, -90). Dans ce cas, pourquoi ne pas appeler le paramètre 🐢 ? L'idée est que t peut être n'importe quelle tortue, pas seulement 🐢. Un autre animal qui effectue le même travail que 🐢 peut donc être créé et passé comme argument à square :

🐫 = Turtle()
@svg begin
    square(🐫)
end

Le procédé consistant à incorporer un morceau de code dans une fonction s'appelle l'encapsulation. Le premier avantage de l'encapsulation est d'associer un nom au code, qui sert en quelque sorte de documentation. Un autre avantage résulte du fait que lors de la réutilisation ultérieure du code, il devient plus concis d'appeler une fonction deux fois que d'en « copier-coller » le corps.

L'étape suivante consiste à ajouter un paramètre len à square. Voici une solution :

function square(t, len)
    for i in 1:4
        forward(t, len)
        turn(t, -90)
    end
end

🐢 = Turtle()
@svg begin
    square(🐢, 100)
end

L'ajout d'un paramètre à une fonction s'appelle une généralisation. Dans la version précédente, le carré dessiné présente toujours la même taille. Dans la dernière version, sa taille peut varier.

L'étape suivante est également une généralisation. Au lieu de dessiner des carrés, polygon dessine des polygones réguliers avec un nombre quelconque de côtés. Voici une solution :

function polygon(t, n, len)
    angle = 360 / n

    for i in 1:4
        forward(t, len)
        turn(t, -angle)
    end
end

🐢 = Turtle()
@svg begin
    polygon(🐢, 7, 70)
end

Ce code permet de dessiner un polygone à 7 côtés, chacun d'eux ayant une longueur de 70 pixels.

L'étape suivante consiste à écrire circle, qui prend un rayon, r, comme paramètre. Voici une solution simple qui utilise polygon pour dessiner un polygone à 50 côtés :

function circle(t, r)
    circumference = 2 * π * r
    n = 50
    len = circumference / n
    polygon(t, n, len)
end

La première ligne calcule la circonférence d'un cercle de rayon r en utilisant la formule kitxmlcodeinlinelatexdvp2\pi rfinkitxmlcodeinlinelatexdvp. Le paramètre n est le nombre de segments dans l'approximation d'un cercle, len est donc la longueur de chaque segment. Ainsi, la fonction polygon dessine-t-elle un polygone à 50 côtés qui se rapproche d'un cercle de rayon r.

Une des limites de cette solution vient de ce que n est une constante, ce qui signifie que, pour les très grands cercles, les segments de droite sont trop longs. En revanche, pour les petits cercles, nous perdons du temps à dessiner de très petits segments. Une solution consisterait à généraliser la fonction en prenant n comme paramètre. Cela donnerait à l'utilisateur (celui qui appelle circle) plus de contrôle, mais l'interface serait moins propre.

L'interface d'une fonction est un résumé de son utilisation : quels sont les paramètres ? Que fait la fonction ? Quelle est la valeur retournée ? Une interface est « propre » si elle permet à l'utilisateur de faire ce qu'il souhaite sans avoir à s'occuper de détails inutiles.

Dans cet exemple, r est un membre de l'interface, car ce paramètre conditionne le cercle à dessiner. Le paramètre n est moins approprié dans la mesure où il concerne les détails relatifs à la façon dont le cercle doit être rendu.

Plutôt que d'encombrer l'interface, il est préférable de choisir une valeur appropriée de n en fonction de la circonférence :

function circle(t, r)
    circumference = 2 * π * r
    n = trunc(circumference / 3) + 3
    len = circumference / n
    polygon(t, n, len)
end

Désormais, le nombre de segments est un nombre entier proche de la valeur de circumference / 3 et la longueur de chaque segment vaut 3. Cette valeur est un bon compromis : assez petite pour que les cercles présentent une allure convenable, tout en étant assez grande pour être efficace et, qui plus est, acceptable pour toute taille de cercle. L'addition de 3 à n garantit que le polygone ait au moins trois côtés.

Quand nous avons écrit circle, il a été possible de réutiliser polygon, car un polygone à grand nombre de côtés est une bonne approximation d'un cercle. Si nous voulions tracer un arc, pourrait-on utiliser polygon ou circle ? Cela demande un peu de travail.

Une possibilité est de commencer avec une copie de polygon et de la transformer en arc. Le résultat ressemblerait à ceci :

function arc(t, r, angle)
    arc_length = 2 * π * r * (angle / 360)
    n = trunc(arc_len / 3) + 1
    step_len = arc_len / n
    step_angle = angle / n
    for i in 1:n
        forward(t, step_len)
        turn(t, -step_angle)
    end
end

La deuxième moitié de cette fonction ressemble à polygon. Malheureusement, on ne peut pas réutiliser polygon sans en changer l'interface. Nous pourrions généraliser polygon pour prendre un angle comme troisième argument. Cependant, polygon ne serait plus un nom approprié. En conséquence, renommons de manière plus générale cette fonction en polyline :

function polyline(t, n, len, angle)
    for i in 1:n
        forward(t, len)
        turn(t, -angle)
    end
end

À présent, nous pouvons réécrire polygon et arc pour tirer parti de polyline :

function polygon(t, n, len)
    angle = 360 / n
    polyline(t, n, len, angle)
end

function arc(t, r, angle)
    arc_length = 2 * π * r * (angle / 360)
    n = trunc(arc_len / 3) + 1
    step_len = arc_len / n
    step_angle = angle / n
    polyline(t, n, step_len, step_angle)
end

Enfin, nous pouvons réécrire circle afin d'utiliser arc :

function circle(t, r)
    arc(t, r, 360)
end

Ce processus, qui consiste à réorganiser un programme pour améliorer les interfaces et faciliter la réutilisation du code, s'appelle la refonte (ou refactoring). Dans le cas présent, nous avons remarqué un code similaire dans arc et polygon, nous l'avons donc « remanié » (refondu) en polyline.

Si nous avions planifié la programmation, nous aurions peut-être écrit polyline au premier jet et évité la refonte. Souvent au début d'un projet, on n'en connait pas assez pour concevoir les interfaces optimales. Lorsqu'on entame le codage, le problème est mieux cerné. Parfois, la refonte est le signe d'une compréhension approfondie d'un problème.

Un plan de développement est un processus de rédaction de programmes. Celui que nous avons utilisé dans cette étude de cas est constitué de deux étapes : l'encapsulation et la généralisation.

Les étapes de ce processus sont les suivantes :

1. Commencer par écrire un petit programme sans définition de fonction ;
2. Une fois le programme opérationnel, identifier une partie cohérente de celui-ci. L'encapsuler dans une fonction et le nommer ;
3. Généraliser la fonction en ajoutant les paramètres appropriés ;
4. Répéter les étapes 1 à 3 jusqu'à obtenir un ensemble de fonctions opérationnelles. Copier et coller le code de travail (pour éviter des saisies et déboguer à nouveau) ;
5. Chercher des possibilités d'améliorer le programme en le remaniant (processus de refonte). Par exemple, avec un code similaire à plusieurs endroits, envisager de le refondre dans une fonction générale idoine.

Cette manière de procéder présente quelques inconvénients — nous verrons les autres options plus tard —, mais il s'avère utile si le programmeur ignore comment diviser le programme en fonctions. Cette approche permet de concevoir un programme de manière progressive.

Une documentation interne brève (docstring) est un bloc de commentaires situé avant une fonction pour en expliciter l'interface :

"""
Draws n line segments with the given length and
angle (in degrees) between them. t is a turtle.
"""
function polyline(t, n, len, angle)
    for i in 1:n
        forward(t, len)
        turn(t, -angle)
    end
end

On peut accéder à la documentation dans le REPL en saisissant le caractère ? suivi du nom d'une fonction ou d'une macro et en appuyant sur ENTER :

help?> polyline
search

    polyline(t, n, len, angle)
    Draws n line segments with the given length and angle (in degrees) between them. t is a turtle.

La documentation brève consiste souvent en des chaînes précédées et suivies d'un triple ", également appelées chaînes multilignes, car les triples guillemets permettent à la chaîne de s'étendre sur plus d'une ligne.

Une interface s'apparente à un « contrat » entre une fonction et un appelant. L'appelant accepte de fournir certains paramètres et la fonction consent à effectuer certains travaux.

Par exemple, polyline nécessite quatre arguments : t doit être de « type » Turtle, n un nombre entier, len un nombre positif et angle un nombre exprimé en degrés.

Ces exigences sont appelées conditions préalables (ou a priori), car elles sont supposées être vraies avant que la fonction ne commence à s'exécuter. A contrario, les conditions résultant de l'exécution de la fonction sont dites a posteriori. Ces conditions a posteriori comprennent l'effet prévu de la fonction (comme les segments de ligne de dessin) et tout effet secondaire (comme le déplacement de la tortue ou d'autres modifications). Les conditions préalables sont de la responsabilité de l'appelant. Si l'appelant viole une condition préalable (correctement documentée) et que la fonction ne donne pas le résultat attendu, le bogue se trouve chez l'appelant et non dans la fonction. Si les conditions préalables sont satisfaites et que les conditions a posteriori ne le sont pas, le bogue se trouve dans la fonction. Si les conditions préalables et les conditions a posteriori sont claires, elles peuvent aider au débogage.

module fichier qui contient une collection de fonctions connexes et diverses définitions.

paquet bibliothèque externe avec des fonctionnalités supplémentaires.

déclaration d'utilisation déclaration qui lit un fichier de module et crée un objet de module.

boucle partie d'un programme qui peut être exécutée de manière répétitive.

encapsulation processus de transformation d'une séquence d'instructions en une définition de fonction.

généralisation processus consistant à remplacer un élément inutilement spécifique (comme un nombre) par élément suffisamment général (comme une variable ou un paramètre).

interface description de la manière d'utiliser une fonction, y compris le nom ainsi que la description des arguments et de la valeur de retour.

refonte (refactoring) processus de modification d'un programme pour améliorer les interfaces des fonctions et d'autres qualités du code.

plan de développement processus de conception et de rédaction de programmes.

documentation courte (docstring) chaîne qui apparaît juste avant la définition d'une fonction pour documenter l'interface de cette dernière.

condition préalable (ou a priori) exigence qui doit être satisfaite par l'appelant avant le début d'une fonction.

condition a posteriori exigence qui doit être satisfaite par la fonction avant qu'elle ne prenne fin.

4-12-1. Exercice 4-8▲

"""
Trace un arc d'un rayon et d'un angle donnés:
    t: turtle
    r: rayon
    angle: angle sous-tendu par l'arc, en degrés
"""
function arc(t, r, angle)
    arc_len = 2 * π * r * abs(angle) / 360
    n = trunc(arc_len / 4) + 3
    step_len = arc_len / n
    step_angle = angle / n

    # faire un léger virage à gauche avant de démarrer
    # réduit l'erreur causée par l'approximation linéaire de l'arc
    turn(t, -step_angle/2)
    polyline(t, n, step_len, step_angle)
    turn(t, step_angle/2)
end

4-12-2. Exercice 4-9▲

Rédigez un ensemble de fonctions générales appropriées pour dessiner des fleurs telles que celles-ci :

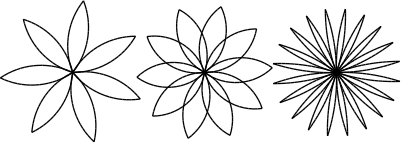
4-12-3. Exercice 4-10▲

Rédigez un ensemble de fonctions générales appropriées pour dessiner des formes :

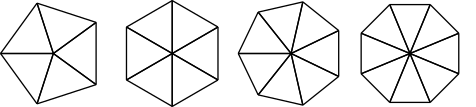
4-12-4. Exercice 4-11▲

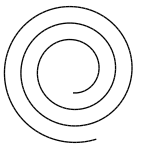
4-12-5. Exercice 4-12▲

Consultez cette page Wikipédia afin d'apprendre des informations sur les spirales. Ensuite, écrivez un programme qui dessine une spirale d'Archimède telle que ceci :