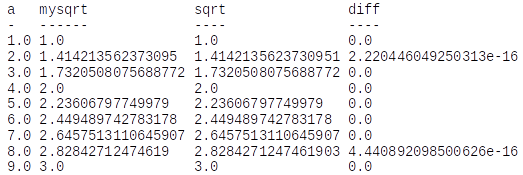Think Julia

Comme le lecteur l'a certainement observé, il est permis de faire plus d'une affectation à la même variable. Une nouvelle affectation fait en sorte qu'une variable existante se réfère à une nouvelle valeur et, en conséquence, cesse de se référer à l'ancienne valeur.

julia> x = 5
5
julia> x = 7
7

La première fois que nous affichons x, sa valeur est de 5 ; la deuxième fois, sa valeur est de 7. La réaffectation peut se représenter dans un diagramme d'état comme suit :

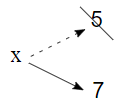
À ce stade, il est temps d'aborder une source commune de confusion. Du fait que Julia utilise le signe égal = pour l'affectation, il est tentant d'interpréter une déclaration telle que a = b comme une proposition mathématique d'égalité, c'est-à-dire l'affirmation que a et b sont égaux. Cette interprétation est erronée.

Premièrement, l'égalité est une relation symétrique. L'affectation ne l'est pas. Par exemple, en mathématiques, si a = 7, il est permis d'écrire 7 = a. Dans Julia, l'énoncé a = 7 est licite ; 7 = a ne l'est pas.

En outre, en mathématiques, une proposition d'égalité est soit vraie soit fausse ad vitam. Si a = b maintenant, alors a sera toujours égal à b. Dans Julia, une déclaration d'affectation peut rendre deux variables égales, mais elles ne doivent pas nécessairement le rester éternellement.

julia> a = 5
5
julia> b = a        # a et b pointent vers la même valeur 5
5
julia> a = 3        # a ne pointe plus vers 5, mais vers 3
3
julia> b            # b pointe toujours vers 5
5

La troisième ligne modifie la valeur de a, mais ne change pas la valeur de b, de sorte qu'elles ne sont plus égales.

Il est courant de réaffecter une variable via la mise à jour de son ancienne valeur :

julia> x = x + 1
8

Cela signifie « obtenir la valeur actuelle de x (à savoir 7), y ajouter 1 et ensuite affecter 8 à x ».

Lors d'une tentative de mise à jour d'une variable non déclarée, Julia retourne une erreur :

julia> y = y + 1
ERROR: UndefVarError: y not defined

Avant de pouvoir mettre à jour une variable, il est impératif de l'initialiser, généralement grâce à une simple affectation :

julia> y = 0
0
julia> y = y +1
1

Les ordinateurs sont souvent utilisés pour automatiser les tâches répétitives. Répéter des tâches identiques ou similaires sans faire d'erreur constitue un point fort des ordinateurs, contrairement aux humains. Dans un programme informatique, la répétition est également appelée itération.

Nous avons déjà vu deux fonctions, countdown et printn, qui utilisent la récursion (section 5.8Récursion). Comme l'itération est très courante, Julia propose des fonctions pour la rendre plus facile d'utilisation. L'une d'entre elles est la déclaration for que nous avons vue dans la section 4.2Répétitions simples. Nous y reviendrons ultérieurement.

while constitue une autre déclaration. Voici une version de countdown exploitant la déclaration while :

function countdown(n)
    while n > 0
        print(n, " ")
        n = n - 1
    end
    println("mise à feu !")
end

Cette déclaration while peut quasiment être lue comme si elle était formulée en langage naturel : « Si n est supérieur à 0, affichez la valeur de n, puis décrémentez n. Lorsque vous arrivez à 0, affichez l'expression "mise à feu !" ».

De manière un peu plus formelle, voici le déroulement de l'instruction while :

1. Déterminer si la condition est vraie ou fausse ;
2. Si elle est fausse, quitter la déclaration while et continuer l'exécution à l'instruction suivante ;
3. Si la condition est vraie, exécuter le corps et revenir ensuite à l'étape 1.

Ce type de flux est appelé une boucle, car la troisième étape revient en boucle vers le haut. Il est fondamental que le corps de la boucle modifie la valeur d'une ou plusieurs variables, de sorte que la condition devienne fausse à terme et que la boucle se termine. Sinon, celle-ci se répète indéfiniment (boucle infinie).(14)

Dans le cas de countdown, on peut prouver que la boucle se termine : si n est nul ou négatif, la boucle ne se répète jamais. Sinon, n est décrémenté à chaque passage dans la boucle, de sorte que n finit par valoir 0. Pour certaines autres boucles, ce n'est pas si facile à identifier. Par exemple :

function seq(n)
    while n != 1
        println(n)
        if n % 2 == 0      # n est pair
            n = n /2
        else               # n est impair
            n = n*3 + 1
        end
    end
end

La condition pour cette boucle est n != 1, donc la boucle continue jusqu'à ce que n vaille 1 (ce qui rend la condition fausse). À chaque fois que la boucle se poursuit, le programme fournit la valeur de n et vérifie ensuite si elle est paire ou impaire. S'il est pair, n est divisé par 2 tandis que, s'il est impair, la valeur de n est remplacée par n*3 + 1. Par exemple, si l'argument passé à la séquence vaut 3, les valeurs résultantes de n sont 3, 10, 5, 16, 8, 4, 2, 1.

Comme n augmente parfois et qu'il diminue parfois, il n'y a pas de preuve évidente que n atteindra 1 ou que le programme se termine. Pour certaines valeurs particulières de n, nous pouvons prouver la fin du programme. Par exemple, si la valeur de départ est une puissance de deux, n sera pair à chaque passage dans la boucle jusqu'à ce qu'il atteigne 1. L'exemple précédent se termine par une telle séquence, en commençant par 16.

La question véritablement difficile est de savoir s'il peut être prouvé que ce programme se termine pour toutes les valeurs positives de n. Jusqu'à présent, personne n'a été capable ni de prouver ni de réfuter cet énoncé. Il s'agit de la conjecture de Collatz.

7-3-1. Exercice 7-1▲

Parfois, on ne sait pas qu'il est temps de terminer une boucle avant d'avoir parcouru la moitié du corps. Dans ce cas, l'instruction break peut être utilisée pour sortir de la boucle. Supposons, par exemple, qu'il faille capter les données d'un utilisateur jusqu'à ce que celui-ci saisisse « done ». Voici un exemple :

while true
    print("> ")
    line = readline()
    if line == "done"
        break
    end
    println(line)
end
println("Done!")

La boucle conditionnelle est toujours vraie. Donc, la boucle se déroule jusqu'à ce qu'elle atteigne l'instruction break.

À chaque passage, la boucle présente une invite > à l'utilisateur. Si l'utilisateur saisit le terme done, l'instruction break force la sortie de la boucle. Sinon, le programme retourne la saisie de l'utilisateur et, ensuite, il revient au début de la boucle. Voici un exemple d'exécution :

> not done
not done
> done
Done!

Cette manière d'écrire des boucles while est courante, car on peut vérifier la condition n'importe où dans la boucle (pas seulement en haut) et la condition d'arrêt peut être exprimée affirmativement (« arrêtez quand cela se produit ») plutôt que négativement (« continuez tant que cela ne se produit pas »).

L'instruction break force la sortie d'une boucle. Lorsque l'instruction continue est rencontrée à l'intérieur d'une boucle, l'exécution saute au début de la boucle afin d'entamer l'itération suivante. Donc, l'exécution des instructions à l'intérieur du corps de la boucle est contournée. Par exemple :

for i in 1:10
    if i % 3 == 0
        continue
    end
    print(i, " ")
end

Julia retourne :

1 2 4 5 7 8 10

Si i est divisible par 3, l'instruction continue arrête l'itération en cours et l'itération suivante commence. Seuls les nombres compris entre 1 et 10 non divisibles par 3 sont affichés.

Les boucles sont souvent utilisées dans les programmes qui traitent des résultats numériques en commençant par une réponse approximative et en l'améliorant de manière itérative pour converger vers la solution.

Par exemple, la méthode de Newton permet de calculer les racines carrées. Supposons que nous souhaitons connaître la racine carrée d'un nombre kitxmlcodeinlinelatexdvp\alphafinkitxmlcodeinlinelatexdvp. En commençant avec presque n'importe quelle estimation x, il est possible calculer une meilleure estimation avec la formule suivante :

Si kitxmlcodeinlinelatexdvp\alphafinkitxmlcodeinlinelatexdvp = 4 et x = 3 (kitxmlcodeinlinelatexdvp\alphafinkitxmlcodeinlinelatexdvp s'obtient par \alpha TAB et ainsi de suite pour tout l'alphabet grec) :

julia> α = 4
4
julia> x =3
3
julia> y = (x + α/x) / 2
2.1666666666666665

Par rapport à la valeur initiale introduite (x = 3), le résultat s'approche davantage de kitxmlcodeinlinelatexdvp\sqrt{4}=2finkitxmlcodeinlinelatexdvp. Après une répétition, le calcul converge vers la solution :

julia> x = y
2.1666666666666665
julia> y = (x + α/x) / 2
2.0064102564102564

Après quelques itérations manuelles, l'estimation devient presque exacte :

julia> x = y
2.0064102564102564
julia> y = (x + α/x) / 2
2.0000102400262145
julia> x = y
2.0000102400262145
julia> y = (x + α/x) / 2
2.0000000000262146

En général, le nombre d'itérations nécessaires pour obtenir la bonne réponse est a priori inconnu. En revanche, lorsque la valeur de l'estimation ne change plus, le calcul peut être arrêté :

julia> x = y
2.0000000000262146
julia> y = (x + α/x) / 2
2.0
julia> x = y
2.0
julia> y = (x + α/x) / 2
2.0

C'est le cas quand y == x. Voici une boucle qui commence avec une estimation initiale, x, et qui améliore celle-ci jusqu'à ce que le résultat cesse de changer :

while true
    println(x)
    y = (x + α/x) / 2
    if y == x
        break
    end
    x = y
end

Pour la plupart des valeurs, ce code fonctionne bien. Cependant, en général, il est dangereux de tester l'égalité de nombres à virgules flottantes. Les valeurs à virgule flottante ne sont qu'approximativement correctes : la plupart des nombres rationnels, comme kitxmlcodeinlinelatexdvp\frac{1}{3}finkitxmlcodeinlinelatexdvp, et les nombres irrationnels, comme kitxmlcodeinlinelatexdvp\sqrt{2}finkitxmlcodeinlinelatexdvp, ne peuvent pas être représentés exactement par un Float64.

Plutôt que de vérifier si x et y sont rigoureusement égaux, il est plus sûr d'utiliser la fonction interne abs pour calculer la valeur absolue de leur différence :

if abs(x - y) < ε
    break
end

Dans ce code, ε (\varepsilon TAB) a une valeur telle que 0,000 000 1 qui détermine la proximité au résultat réel.

La méthode de Newton est un exemple d'algorithme. Il s'agit d'un processus mécanique pour résoudre une catégorie de problèmes (dans ce cas, le calcul de racines carrées).

Pour comprendre ce qu'est un algorithme, il peut être utile de commencer par un procédé qui ne relève pas d'un algorithme. Pour apprendre la multiplication des nombres à un chiffre, il est nécessaire de mémoriser les tables de multiplication avec 100 solutions spécifiques. Ce type de connaissance n'est pas algorithmique.

Toutefois, un individu « paresseux » aurait peut-être appris quelques astuces. Par exemple, pour trouver le produit de n et 9, il est possible d'écrire kitxmlcodeinlinelatexdvpn-1finkitxmlcodeinlinelatexdvp comme premier chiffre et kitxmlcodeinlinelatexdvp10-nfinkitxmlcodeinlinelatexdvp comme deuxième chiffre. Cette astuce est une solution générale pour multiplier tout nombre à un chiffre par 9 : il s'agit d'un algorithme.

De même, les techniques apprises à l'école primaire pour l'addition avec report, la soustraction par emprunt (ou celle par compensation) et la division longue (méthode de la potence) sont toutes de nature algorithmique. Les algorithmes ont pour caractéristique commune de ne nécessiter aucune intelligence pour être exécutés. Ce sont des processus mécaniques où chaque étape suit la précédente selon un ensemble de règles simples.

Exécuter des algorithmes est ennuyeux, mais les concevoir est intéressant, intellectuellement stimulant et constitue une part centrale de l'informatique.

Certains actes naturellement exécutés par les humains, sans difficulté ni pensée consciente, sont les plus difficiles à exprimer par des algorithmes. La compréhension du langage naturel en est un bon exemple. Nous agissons tous ainsi, mais, jusqu'à présent, personne n'a pu expliquer comment nous pratiquons, du moins pas sous la forme d'un algorithme.

Plus la taille des programmes augmente, plus de temps de débogage s'allonge. Davantage de code signifie davantage de risques d'erreur et plus d'endroits où les bogues peuvent se camoufler.

Le « débogage par bissection » est une des méthodes permettant de réduire le temps de débogage. Par exemple, s'il y a 100 lignes dans un programme et qu'elles sont vérifiées une à une, il en résultera 100 étapes. Il est plus astucieux de diviser le problème en deux en regardant vers le milieu du programme pour capter une valeur intermédiaire vérifiable. Il suffit d'ajouter une instruction d'affichage (ou quelque technique vérifiable) et lancer le programme. Si la vérification intermédiaire est incorrecte, le problème se situe dans la première moitié du programme. Si la vérification est correcte, le problème se situe dans la seconde moitié.

Chaque fois qu'un contrôle de ce type est utilisé, le nombre de lignes à analyser est divisé par deux. Pour 100 lignes de codes et après seulement six étapes, il n'y a plus qu'une ou deux lignes de code à vérifier, du moins en théorie.

Dans la pratique, il n'est pas toujours aisé de déterminer le « milieu du programme » et une vérification n'est pas toujours réalisable. Il n'est pas pertinent de compter les lignes et de trouver l'exact milieu. Mieux vaut repérer les endroits du programme où des erreurs pourraient apparaître et où il est facile de pratiquer une vérification. Ensuite, il est judicieux de choisir un endroit où les chances de débusquer le bogue avant ou après la vérification sont approximativement les mêmes.

réaffectation attribution d'une nouvelle valeur à une variable qui existe déjà.

mise à jour affectation où la nouvelle valeur de la variable dépend de l'ancienne.

initialisation affectation qui donne une valeur initiale à une variable qui sera mise à jour ultérieurement.

incrémentation mise à jour qui augmente la valeur d'une variable (typiquement de 1).

décrémentation mise à jour qui diminue la valeur d'une variable (typiquement de 1).

itération exécution répétée d'un ensemble d'instructions en utilisant soit un appel de fonction récursif, soit une boucle.

while instruction qui permet des itérations contrôlées par une condition.

break instruction permettant de sortir d'une boucle.

continue instruction à l'intérieur d'une boucle qui provoque un saut au début de la boucle pour l'itération suivante.

boucle infinie boucle dans laquelle la condition de fin n'est jamais remplie.

algorithme processus général pour résoudre une catégorie de problèmes.

7-10-1. Exercice 7-2▲

7-10-2. Exercice 7-3▲

julia> expr = Meta.parse("1+2*3")
:(1 + 2 * 3)
julia> eval(expr)
7
julia> expr = Meta.parse("sqrt(π)")
:(sqrt(π))
julia> eval(expr)
1.7724538509055159

7-10-3. Exercice 7-4▲