Think Julia

Dans un paquet, il y a cinquante-deux cartes, chacune appartenant à une des quatre couleurs et à un des treize rangs (ou hauteurs, voir l'exercice 18.13.3Exercice 18-6). Au poker, les couleurs sont pique (♠), cœur (♥), carreau (♦) et trèfle (♣). Les rangs sont : as (A), 2, 3, 4, 5, 6, 7, 8, 9, 10, valet (J(45)), dame (Q) et roi (K). Selon le jeu auquel on participe, un as peut être supérieur au roi ou inférieur à 2.

Si nous souhaitons définir un nouvel objet pour représenter une carte à jouer, il est évident que les attributs doivent être le rang et la couleur. En revanche, le type de ces attributs n'est pas aussi intuitif à déterminer. Une option consiste à utiliser des chaînes de caractères contenant des mots comme « pique » pour les couleurs et « dame » pour les rangs. Un problème relatif à cette mise en œuvre provient de la difficulté de comparer les cartes en termes de préséance de rang ou de couleur.

Une autre option consiste à utiliser des nombres entiers pour coder les rangs et les couleurs. Dans ce contexte, « coder » signifie que nous allons définir une correspondance entre des nombres et les couleurs ainsi qu'entre des nombres et les rangs. Ce type de codage n'est pas secret, autrement, il s'agirait d'un chiffrement.

Par exemple, ce tableau illustre la correspondance « couleurs kitxmlcodeinlinelatexdvp\mapstofinkitxmlcodeinlinelatexdvp nombres entiers » :

• ♠ kitxmlcodeinlinelatexdvp\mapstofinkitxmlcodeinlinelatexdvp 4
• ♥ kitxmlcodeinlinelatexdvp\mapstofinkitxmlcodeinlinelatexdvp 3
• ♦ kitxmlcodeinlinelatexdvp\mapstofinkitxmlcodeinlinelatexdvp 2
• ♣ kitxmlcodeinlinelatexdvp\mapstofinkitxmlcodeinlinelatexdvp 1

Cette correspondance permet de comparer facilement les cartes. La hiérarchie des couleurs correspond à la hiérarchie des nombres. Nous procédons de la même manière pour les rangs avec 13 nombres (13 kitxmlcodeinlinelatexdvp\mapstofinkitxmlcodeinlinelatexdvp roi, 12 kitxmlcodeinlinelatexdvp\mapstofinkitxmlcodeinlinelatexdvpdame, etc.).

Le symbole kitxmlcodeinlinelatexdvp\mapstofinkitxmlcodeinlinelatexdvp est employé pour indiquer clairement que ces correspondances ne font pas partie du programme Julia. Elles relèvent de la conception du programme, sans toutefois apparaître explicitement dans le code.

La définition de la struct pour Carte se présente de cette manière :

struct Carte 
    couleur :: Int64 
    rang :: Int64 
    function Carte(couleur::Int64, rang::Int64) 
         @assert(1 ≤ couleur ≤ 4, "la couleur n'est pas entre 1 et 4")
         @assert(1 ≤ rang ≤ 13, "le rang n'est pas entre 1 et 13") 
    new(couleur, rang)
    end 
end

Pour créer une carte, nous appelons Carte avec la couleur et le rang souhaités :

julia> dame_de_carreau = Carte(2, 12)
Carte(2, 12)

Afin d'afficher les objets Carte de sorte que tout le monde puisse les lire facilement, il faut établir une correspondance entre les couleurs et leurs entiers ainsi qu'une correspondance entre les rangs et leurs entiers. Une manière naturelle de procéder consiste à utiliser deux tableaux de chaînes de caractères(46) :

const noms_couleurs = ["♣", "♦", "♥", "♠"] 
const noms_rangs = ["A", "2", "3", "4", "5", "6", "7", "8", "9", "10", "V", "D", "R"]

Les variables noms_couleurs et noms_rangs sont globales. La déclaration const signifie que la variable ne peut être attribuée qu'une seule fois. Cela résout le problème de la performance des variables globales.

Dès lors, nous pouvons mettre en œuvre une méthode show idoine :

function Base.show(io::IO, carte::Carte)
    print(io, noms_rangs[carte.rang], noms_couleurs[carte.couleur])
end

L'expression noms_rangs[carte.rang] signifie « utiliser le champ rang de l'objet carte comme indice dans le tableau noms_rangs et sélectionner la chaîne appropriée ».

Avec les méthodes dont nous disposons à ce stade, nous pouvons créer et afficher des cartes :

julia> Carte(3, 11)
V♥

Pour les types internes, il existe des opérateurs relationnels (<, >, ==, etc.) qui comparent les valeurs et déterminent quand l'une est supérieure, inférieure ou égale à l'autre. Pour les types définis par le programmeur, nous pouvons remplacer le comportement des opérateurs intégrés en fournissant une méthode nommée : <.

La préséance correcte des cartes n'est pas évidente. Par exemple, du 3 de trèfle ou du 2 de carreau qui l'emporte ? L'un a un rang plus élevé, mais l'autre a une couleur plus élevée. Pour comparer les cartes, il faut décider si c'est le rang ou la couleur qui l'emporte.

La réponse peut dépendre du jeu. Pour simplifier, nous supposons que la couleur a priorité sur le rang. De la sorte, toutes les piques l'emportent sur toutes les carreaux, etc. Ainsi, dans l'exemple cité au début de cette section, 3♣ < 2♦.

Ceci fixé, nous pouvons écrire < :

import Base.<

function <(c1::Carte, c2::Carte)
    (c1.couleur, c1.rang) < (c2.couleur, c2.rang)
end

18-3-1. Exercice 18-1▲

Les tests unitaires (T.U.) permettent de vérifier l'exactitude d'un code en comparant les résultats effectifs de ce dernier à ce qu'on en attend. Cela peut être utile pour s'assurer que le code est toujours correct après modifications. Cette technique est aussi une manière de prédéfinir le comportement correct du code pendant la phase de développement.

Des tests unitaires simples peuvent être effectués avec les macros @test :

julia> using Test

julia> @test Carte(1, 4) < Carte(2, 4)
Test Passed
julia> @test Carte(1, 3) < Carte(1, 4)
Test Passed

@test retourne « Test Passed » si l'expression est true, « Test Failed » si elle est false et « Error Result » si elle ne peut pas être évaluée.

Maintenant que nous avons les cartes, l'étape suivante consiste à créer des paquets de cartes. Il est naturel que chaque paquet contienne un tableau de cartes comme attribut.

Voici une structure composite de Paquet. Le constructeur crée les cartes des champs et produit un jeu de 52 cartes :

struct Paquet 
    cartes :: Array{Carte, 1} 
end

function Paquet() 
    paquet = Paquet(Carte[]) 
    for couleur in 1:4 
        for rang in 1:13 
            push!(paquet.cartes, Carte(couleur, rang)) 
        end
    end
    paquet
end

La manière la plus simple de constituer un paquet consiste à utiliser deux boucles. La boucle extérieure permet de créer les couleurs (de 1 à 4) et la boucle intérieure permet de produire les rangs (de 1 à 13). Chaque itération crée une nouvelle carte qui entre dans paquet.cartes. Ainsi, la première carte produite est l'as de trèfle, puis le 2 de trèfle, etc., jusqu'à la dernière carte, le roi de pique.

Voici la méthode show pour Paquet :

function Base.show(io::IO, paquet::Paquet) 
    for carte in paquet.cartes
        print(io, carte, " ")
    end
    println()
end

Voici le résultat :

julia> Paquet()
A♣ 2♣ 3♣ 4♣ 5♣ 6♣ 7♣ 8♣ 9♣ 10♣ V♣ D♣ R♣ A♦ 2♦ 3♦ 4♦ 5♦ 6♦ 7♦ 8♦ 9♦ 10♦ V♦ D♦ R♦ A♥ 2♥ 3♥ 4♥ 5♥ 6♥ 7♥ 8♥ 9♥ 10♥ V♥ D♥ R♥ A♠ 2♠ 3♠ 4♠ 5♠ 6♠ 7♠ 8♠ 9♠ 10♠ V♠ D♠ R♠

Pour distribuer des cartes, il faudrait pouvoir utiliser une fonction qui retire une carte du jeu et l'affiche. La fonction pop! est utile à cet égard :

function Base.pop!(paquet::Paquet) 
    pop!(paquet.cartes)
end

Vu son mode d'action (retrait du dernier élément d'une structure de données), pop! agit sur le bas de la pile.

Ajouter une carte peut se faire en utilisant la fonction push! :

function Base.push!(paquet::Paquet, carte::Carte) 
    push!(paquet.cartes, carte)
    paquet 
end

Une telle méthode qui exploite une autre méthode en n'effectuant que peu de traitement supplémentaire s'appelle du placage. La métaphore vient de la marqueterie, où un placage est une fine couche de bois noble collée à la surface d'une pièce de bois de moindre qualité afin d'en améliorer l'apparence.

Dans ce cas, push! est une méthode « légère » qui adapte une opération sur les tableaux au cas des paquets de cartes. Elle améliore l'interface de l'implémentation.

Comme autre exemple, pour battre les cartes, nous pouvons écrire une méthode appelée shuffle! en utilisant la fonction Random.shuffle! :

using Random
function Random.shuffle!(paquet::Paquet)
    shuffle!(paquet.cartes)
    paquet
end

18-6-1. Exercice 18-2▲

Pour jouer aux cartes, il faut créer une « main », c'est-à-dire un ensemble de cartes détenues par un joueur. Pour cela, il est nécessaire d'y associer un type. Or, une main est similaire à un jeu de cartes : les deux sont composés d'une collection de cartes et les deux recourent à des opérations comme l'ajout et le retrait de cartes.

Toutefois, il existe des différences. Certaines opérations spécifiques aux mains n'ont pas de sens pour un jeu de cartes complet. Par exemple, au poker, on peut comparer deux mains pour déterminer laquelle est gagnante. Au bridge, on peut calculer le score d'une main pour faire une offre.

Nous devons donc trouver un moyen de regrouper les types spécifiques lorsqu'ils sont apparentés. En Julia, et pour notre problème, la technique consiste à définir un type abstrait qui sert de parent à la fois pour le paquet de cartes complet (Paquet) et pour une main (UneMain(47)). Cette manière de procéder s'appelle le sous-typage.

Nommons le type abstrait EnsembleDeCartes :

abstract type EnsembleDeCartes end

Un nouveau type abstrait est créé avec le mot-clé abstract type. Dans la déclaration que nous venons de faire, un type « parent » peut être facultativement spécifié en précisant (après le nom) le symbole <: suivi lui-même du nom d'un type abstrait existant.

Lorsqu'aucun supertype n'est indiqué, Julia utilise le supertype par défaut Any, un type abstrait prédéfini. Tous les objets en sont des instances. Tous les types en sont des sous-types.

À présent, exprimons que Paquet est un sous-type descendant du type abstrait EnsembleDeCartes :

struct Paquet <: EnsembleDeCartes 
    cartes :: Array{Carte, 1} 
end

function Paquet() 
    paquet = Paquet(Carte[]) 
    for couleur in 1:4 
        for rang in 1:13 
            push!(paquet.cartes, Carte(couleur, rang))
        end 
    end 
    paquet 
end

L'opérateur isa vérifie si un objet est d'un type donné :

julia> paquet = Paquet();

julia> paquet isa EnsembleDeCartes
true

Une main est aussi un sous-type du type parent EnsembleDeCartes :

struct UneMain <: EnsembleDeCartes 
    cartes :: Array{Carte, 1} 
    label :: String 
end

function UneMain(label::String="") 
    UneMain(Carte[], label) 
end

Au lieu de peupler une main avec 52 nouvelles cartes, le constructeur associé à UneMain initialise cartes sous la forme d'un tableau vide. Un argument optionnel peut être passé au constructeur, ce qui permet de donner une étiquette à UneMain.

julia> main = UneMain("nouvelle main")
UneMain(Carte[], "nouvelle main")

Ceci fait (section 18.7Types abstraits et sous-typage), nous pouvons écrire les opérations communes à Paquet et UneMain comme des fonctions ayant pour argument EnsembleDeCartes :

function Base.show(io::IO, edc::EnsembleDeCartes) 
    for carte in edc.cartes
        print(io, carte, " ")
    end 
end

function Base.pop!(edc::EnsembleDeCartes)
    pop!(edc.cartes)
end

function Base.push!(edc::EnsembleDeCartes, carte::Carte)
    push!(edc.cartes, carte)
    nothing
end

À présent, nous pouvons utiliser pop! et push! pour distribuer une carte :

julia> paquet = Paquet()
julia> shuffle!(paquet)
julia> carte = pop!(paquet)
julia> push!(main, carte)

L'étape suivante consiste naturellement à encapsuler ce code dans une fonction appelée move! :

function move!(edc1::EnsembleDeCartes, edc2::EnsembleDeCartes, n::Int) 
    @assert 1 ≤ n ≤ length(edc1.cartes)
        for i in 1:n
            carte = pop!(edc1)
            push!(edc2, carte)
        end
    nothing
end

La fonction move! prend trois arguments : deux objets EnsembleDeCartes et le nombre de cartes à distribuer. Elle modifie les deux objets EnsembleDeCartes et renvoie nothing.

Dans certains jeux, les cartes sont déplacées d'une main à l'autre alors que, dans d'autres jeux, elles sont échangées depuis une main vers le paquet. La fonction move! est donc utilisable pour ces opérations : edc1 et edc2 peuvent être soit de type Paquet, soit de type UneMain.

Jusqu'à présent, nous avons vu des diagrammes de pile (qui résume l'état d'un programme) et des diagrammes d'objet (qui mettent en évidence les attributs d'un objet et leurs valeurs). Ces diagrammes représentent un instantané de l'exécution d'un programme. En conséquence, ils évoluent au fur et à mesure de l'exécution. Ils sont également très détaillés, voire trop pour certains usages.

Un diagramme de types est une esquisse plus abstraite de la structure d'un programme. Au lieu de dépeindre des objets individuels, il représente de manière synthétique les types et les relations qu'ils entretiennent (voir la figure 18.9.1).

Il existe plusieurs catégories de relation entre les types :

• les objets d'un type spécifique peuvent contenir des références à des objets d'un autre type. Par exemple, chaque Rectangle (voir la section 15.4Rectangles) contient une référence à un Point. Dans le présent chapitre, chaque Paquet contient des références à un tableau de Carte. Ce type de relation est appelé HAS-A, comme dans l'expression en anglais : « a Rectangle has a Point » ;

• un type spécifique peut avoir un type abstrait comme supertype. Cette relation est appelée IS-A, comme dans la formulation en anglais : « UneMain is a kind of EnsembleDeCartes » ;

• un type peut dépendre d'un autre dans la mesure où les objets d'un type prennent les objets du second type comme paramètres ou, alors, utilisent les objets du second type dans le cadre d'un calcul. Ce type de relation est appelé une dépendance.

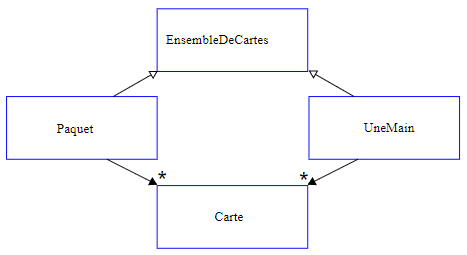
Dans la figure 18.9.1, les flèches à extrémité creuse représentent une relation IS-A. Dans le cas présent, elles indiquent qu'UneMain et Paquet ont comme supertype EnsembleDeCartes.

Les flèches à extrémité pleine représentent une relation HAS-A. Dans le cas présent, Paquet a des références aux objets Carte.

L'étoile (kitxmlcodeinlinelatexdvp\color{blue}\starfinkitxmlcodeinlinelatexdvp) près de la pointe d'une flèche désigne une multiplicité. Elle indique que Paquet ou UneMain possèdent un certain nombre de Cartes. La multiplicité peut être un simple nombre (comme 52), une fourchette (5:7) ou une étoile (kitxmlcodeinlinelatexdvp\color{blue}\starfinkitxmlcodeinlinelatexdvp). Ce dernier cas indique que Paquet peut avoir un nombre quelconque de Cartes.

Il n'y a pas de dépendances dans ce diagramme. Elles sont normalement indiquées par une flèche pointillée. Cependant, si les dépendances sont nombreuses, il est judicieux d'omettre leur représentation.

Un diagramme plus détaillé peut montrer qu'un Paquet contient un tableau de Carte, mais les types internes à Julia comme les tableaux et les dictionnaires ne sont généralement pas repris dans les diagrammes de types.

Le sous-typage peut rendre le débogage difficile. En effet, lorsqu'une fonction est appelée avec un objet comme argument, il peut être compliqué de déterminer quelle méthode est invoquée.

Supposons que nous écrivions une fonction qui manipule des objets UneMain. Idéalement, il faudrait qu'elle fonctionne avec toute sorte de type UneMain, comme PokerUneMain, BridgeUneMain, etc. Si nous invoquons une méthode comme sort!, il se pourrait que nous travaillions effectivement avec celle définie pour le type abstrait UneMain. Toutefois, s'il existe une méthode sort! ayant comme argument un des sous-types, nous manipulerons cette version plutôt que celle définie pour le type abstrait UneMain. Ce comportement est généralement sain, mais, a priori, il peut s'avérer déroutant.

function Base.sort!(main::UneMain)
    sort!(main.cartes)
end

Lorsqu'on n'est pas sûr de la manière dont l'exécution d'un programme procède, la solution la plus simple consiste à ajouter des instructions d'affichage au début des méthodes concernées. Si shuffle! imprime un message tel que « Running shuffle! Paquet », cela signifie que le programme est exécuté correctement.

Une meilleure manière de pratiquer consiste à utiliser la macro @which :

julia> @which sort!(main)
sort!(main::UneMain) in Main at REPL[5]:1

Donc, la méthode sort! associée à main a pour argument un objet de type UneMain.

À ce stade, voici une suggestion relative à la conception d'un programme. Lorsque vous passez outre une méthode, l'interface de la nouvelle méthode doit être la même que l'interface de l'ancienne. Elle devrait prendre les mêmes paramètres, retourner le même type et obéir aux mêmes conditions a priori et a posteriori. Si vous suivez cette règle, vous constaterez que toute fonction conçue pour utiliser une instance d'un supertype (comme EnsembleDeCartes) fonctionnera également avec des instances de ses sous-types (comme Paquet et UneMain).

Si vous enfreignez cette règle, connue comme le « principe de substitution de Liskov », votre code s'effondrera comme un château de cartes.

La fonction supertype peut être utilisée pour trouver le supertype direct d'un type.

julia> supertype(Paquet)
EnsembleDeCartes

Les chapitres 15Structures et objets et 16Structures et fonctions présentent un plan de développement qui pourrait s'appeler « conception orientée type ». Nous avons identifié les objets à traiter — comme Point, Rectangle et MyTime — et nous avons défini des structures pour les représenter. Dans chaque cas, il existait une correspondance évidente entre l'objet et une entité du monde réel (du moins, sa représentation mathématique).

Ceci étant, il est parfois moins facile de déterminer les objets dont nous avons besoin et comment ils doivent interagir. S'il en va ainsi, il faut un plan de développement mieux adapté que la conception orientée type. De la même manière que nous avons découvert les interfaces de fonctions par encapsulation et généralisation, nous allons découvrir les interfaces de types par encapsulation de données.

L'analyse de Markov (section 13.8Analyse de Markov) fournit un bon exemple. Supposons que vous téléchargiez le code sous ce lien. Il est facile de constater que deux variables, suffixes et prefix, sont utilisables en lecture et écriture par plusieurs fonctions.

suffixes = Dict()
prefix = []

Du fait que ces variables sont globales, nous ne pouvons effectuer qu'une seule analyse à la fois. S'il arrivait que deux textes soient lus, leurs préfixes et suffixes seraient ajoutés aux mêmes structures de données (ce qui produirait un texte intéressant).

Pour effectuer plusieurs analyses séparément, il convient d'encapsuler l'état de chaque analyse dans un objet. Voici comment procéder :

struct Markov 
    order :: Int64 
    suffixes :: Dict{Tuple{String,Vararg{String}}, Array{String, 1}}
    prefix :: Array{String, 1} 
end

function Markov(order::Int64=2) 
    new(order, Dict{Tuple{String,Vararg{String}}, Array{String, 1}}(), Array{String, 1}())
end

Ensuite, les fonctions sont transformées en méthodes. Par exemple, voici processword :

function processword(markov::Markov, word::String) 
    if length(markov.prefix) < markov.order 
        push!(markov.prefix, word) 
        return 
    end 
    get!(markov.suffixes, (markov.prefix...,), Array{String, 1}()) 
    push!(markov.suffixes[(markov.prefix...,)], word) 
    popfirst!(markov.prefix)
    push!(markov.prefix, word) 
end

La transformation conduisant à un programme comme celui-ci — à savoir, changer la conception sans modifier le comportement — constitue un autre exemple de refonte (voir la section 4.7Refonte (ou refactoring)).

Cet exemple propose un plan de développement pour la conception des types :

• commencer par écrire des fonctions qui lisent et écrivent des variables globales (si nécessaire) ;
• une fois le programme opérationnel, rechercher les associations entre les variables globales et les fonctions qui les utilisent ;
• encapsuler les variables afférentes sous forme de champs d'une structure composite ;
• transformer les fonctions associées en méthodes avec comme argument les objets du nouveau type.

18-11-1. Exercice 18-3▲

encoder représenter un ensemble de valeurs à l'aide d'un autre ensemble de valeurs en établissant une correspondance entre elles.

test unitaire moyen normalisé de tester l'exactitude d'un code.

placage méthode (ou fonction) qui fournit une interface différente à une autre fonction sans ajouter de calculs supplémentaires.

sous-typage possibilité de définir une hiérarchie de types apparentés.

type abstrait type qui peut agir comme parent pour un autre type.

type spécifique type qui peut être construit à partir d'un type abstrait.

sous-type type qui a comme parent un type abstrait.

supertype type abstrait, parent d'un autre type.

relation IS-A relation entre un sous-type et son supertype.

relation HAS-A relation entre deux types où les instances d'un type contiennent des références aux instances de l'autre.

dépendance relation entre deux types où les instances d'un type utilisent des instances d'un autre type, mais ne les enregistrent pas en tant que champs.

diagramme de type diagramme qui montre les types d'un programme et les relations entre eux.

multiplicité notation dans un diagramme de types qui montre, pour une relation HAS-A, combien de références existent à des instances d'une autre classe.

encapsulation de données plan de développement d'un programme qui comprend un prototype utilisant des variables globales et une version finale transformant les variables globales en champs d'instance.

18-13-1. Exercice 18-4▲

abstract type PingPongParent end

struct Ping <: PingPongParent 
    pong :: PingPongParent 
end

struct Pong <: PingPongParent 
    pings :: Array{Ping, 1} 
    function Pong(pings=Array{Ping, 1}())
        new(pings) 
    end 
end

function addping(pong::Pong, ping::Ping) 
    push!(pong.pings, ping) 
    nothing 
end

pong = Pong() 
ping = Ping(pong)
addping(pong, ping)

18-13-2. Exercice 18-5▲

18-13-3. Exercice 18-6▲