Think Julia

Jusqu'ici, nous avons utilisé de nombreux types internes à Julia. Nous allons maintenant définir un type personnel. À titre d'exemple, nous allons créer un type appelé Point qui représente un point dans un espace bidimensionnel. En notation mathématique, les points sont souvent écrits entre parenthèses avec une virgule séparant les coordonnées. Par exemple, dans un repère cartésien kitxmlcodeinlinelatexdvp\mathbb{R}{}^{2}finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvp(0,0)finkitxmlcodeinlinelatexdvp représente l'origine et kitxmlcodeinlinelatexdvp(x,y)finkitxmlcodeinlinelatexdvp un point dont l'abscisse vaut kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp et l'ordonnée kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp.

Il y a plusieurs façons de traiter cette information en Julia :

1. Les coordonnées pourraient être enregistrées séparément dans deux variables, x et y ;
2. Elles pourraient se retrouver sous forme d'éléments au sein d'un tableau ou d'un tuple ;
3. Enfin, nous pourrions créer un type personnalisé pour représenter les points sous forme d'objets.

La création d'un nouveau type est plus compliquée que les autres options, mais elle présente des avantages qui apparaîtront bientôt.

Un type composite défini par le programmeur est également appelé une structure. La définition struct pour représenter un point ressemble à ceci :

struct Point
    x
    y
end

L'en-tête indique que la nouvelle structure s'appelle Point. Le corps définit les attributs ou les champs de la structure. La structure Point possède deux champs : x et y.

Une structure fonctionne comme une usine créant des objets. Pour créer un point, on peut appeler Point comme s'il s'agissait d'une fonction ayant pour arguments les valeurs des champs. Lorsque Point est utilisé comme une fonction, on l'appelle un constructeur.

julia> p = Point(3.0, 4.0)
Point(3.0, 4.0)

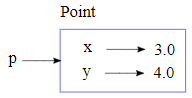
La valeur retournée est une référence à un objet Point, que nous affectons à p. La création d'un nouvel objet est une instanciation et l'objet est une instance du type. Lorsqu'une instance est affichée, Julia indique à quel type elle appartient et quelles sont les valeurs des attributs. Chaque objet est une instance d'un certain type, les termes « objet » et « instance » sont donc interchangeables. Cependant, dans ce chapitre, le terme « instance » sera utilisé pour désigner un type défini par le programmeur.

Un diagramme d'état qui rend compte d'un objet et de ses champs est appelé un diagramme d'objet (voir la figure 15.1.1).

La valeur des champs (ou attributs) peut être extraite en utilisant la notation . de cette manière :

julia> x = p.x
3.0
julia> y = p.y
4.0

L'expression p.x signifie : « Allez à l'objet auquel p se réfère et extrayez la valeur de x ». Dans l'exemple, nous attribuons cette valeur à une variable nommée x. Il n'y a pas de conflit entre la variable x et le champ x.

La notation par points peut être exploitée dans le cadre de n'importe quelle expression. Par exemple, en considérant p.x et p.y comme des longueurs, le théorème de Pythagore est applicable :

julia> distance = sqrt(p.x^2 + p.y^2)
5.0

Ceci dit, par défaut, les structures sont persistantes. Après construction, les champs ne peuvent pas changer de valeur :

julia> p.y = 1.0
ERROR: setfield! immutable struct of type Point cannot be changed

Le caractère persistant des structures présente plusieurs avantages :

• l'efficacité ;

• l'impossibilité de violer les invariants fournis par les constructeurs du type (voir la section 17.4Constructeurs) ;

• la facilité à raisonner sur du code utilisant des objets persistants.

S'il y échet, des types composites non persistants peuvent être déclarés avec le mot-clé mutable struct. Voici la définition d'un point modifiable (MPoint pour « Mutable ») :

mutable struct MPoint
    x
    y
end

Ainsi, il devient possible d'attribuer des valeurs à une instance d'une structure mutable en utilisant la notation par points :

julia> blank = MPoint(0.0, 0.0)
MPoint(0.0, 0.0)
julia> blank.x = 3.0
3.0
julia> blank.y = 4.0
4.0

Régulièrement, les champs d'un objet sont évidents. Néanmoins, dans certaines circonstances, il faut opérer des choix. Imaginons qu'il faille concevoir un type pour représenter des rectangles. Quels champs utiliser afin de spécifier l'emplacement et la taille d'un rectangle ? Pour simplifier les choses, supposons que le rectangle est disposé soit verticalement, soit horizontalement (pour éviter de traiter le problème de son inclinaison).

Il existe au moins deux possibilités :

• nous pouvons définir un coin du rectangle (ou son centre), la largeur et la hauteur ;
• nous pouvons définir deux coins opposés.

À ce stade, il est difficile de dire quel est le meilleur choix. À titre d'exemple, mettons en œuvre le premier cas de figure.

"""
Représentation d'un rectangle.
champs: largeur, hauteur, coin. 
"""
struct Rectangle 
    largeur
    hauteur
    coin
end

La mini-documentation précise les champs : la largeur et la hauteur sont des nombres, tandis que coin (qui requiert deux coordonnées) est un objet Point qui définit le coin inférieur gauche.

Pour représenter un rectangle, il faut instancier un objet Rectangle :

julia> origine = MPoint(0.0, 0.0)
MPoint(0.0, 0.0)
julia> box = Rectangle(100.0, 200.0, origine)
Rectangle(100.0, 200.0, MPoint(0.0, 0.0))

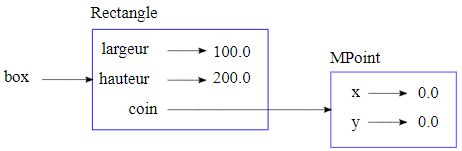
Le diagramme d'objet (voir la figure 15.4.1) montre l'état de l'objet box. Un objet tel que coin, champ d'un autre objet, est dit intégré (embedded). Étant donné que l'attribut coin fait référence à un objet non persistant (MPoint), ce dernier est dessiné en dehors de l'objet Rectangle.

Il est possible de faire passer une instance comme un argument selon la méthode habituelle. Par exemple :

function printpoint(p) 
    println("($(p.x), $(p.y))")
end

printpoint prend une instance Point comme argument et l'affiche en notation mathématique. Pour l'invoquer, vous pouvez passer p comme argument :

julia> printpoint(blank)
(3.0, 4.0)

Si un objet struct non persistant est passé à une fonction en tant qu'argument, cette fonction peut modifier les champs de l'objet. Par exemple, movepoint! prend un objet Point non persistant et deux nombres, dx et dy, et ajoute — respectivement — ces nombres aux attributs x et y de Point :

function movepoint!(p, dx, dy)
    p.x += dx
    p.y += dy 
    nothing
end

Voici un exemple qui en démontre l'effet :

julia> origine = MPoint(0.0, 0.0)
MPoint(0.0, 0.0) 
julia> movepoint!(origine, 1.0, 2.0)

julia> origine 
MPoint(1.0, 2.0)

À l'intérieur de la fonction, p est un alias d'origine. Par conséquent, lorsque la fonction modifie p, l'objet origine est aussi affecté.

Passer un objet Point persistant à movepoint! provoque une erreur :

julia> movepoint!(p, 1.0, 2.0)
ERROR: setfield! immutable struct of type Point cannot be changed

Cependant, il est permis de modifier la valeur d'un attribut non persistant au sein d'un objet persistant. Par exemple, moverectangle! a comme arguments un objet Rectangle et deux nombres (dx et dy). Cette fonction utilise movepoint! pour déplacer le coin du rectangle :

function moverectangle!(rect, dx, dy)
    movepoint!(rect.coin, dx, dy)
end

De ce fait, p dans movepoint! est un alias de rect.coin. Aussi, quand p est modifié, rect.coin l'est-il également :

julia> box 
Rectangle(100.0, 200.0, MPoint(0.0, 0.0)) 
julia> moverectangle!(box, 1.0, 2.0)

julia> box 
Rectangle(100.0, 200.0, MPoint(1.0, 2.0))

julia> box.coin = MPoint(1.0, 2.0)
ERROR: setfield: immutable struct of type Rectangle cannot be changed

15-5-1. Exercice 15-1▲

Les fonctions peuvent renvoyer des instances. Par exemple, findcenter prend Rectangle comme argument et retourne un Point qui contient les coordonnées du centre du rectangle :

function findcenter(rect) 
    Point(rect.coin.x + rect.largeur / 2, rect.coin.y + rect.hauteur / 2)
end

L'expression rect.coin.x signifie : « Allez à l'objet rect et sélectionnez le champ nommé coin, puis rendez-vous à cet objet et sélectionnez le champ nommé x ».

Voici un exemple qui passe box en argument et affecte le Point résultant à centre :

julia> centre = findcenter(box)
Point(51.0, 102.0)

L'aliasing peut rendre un programme difficile à lire, parce que les modifications apportées à un endroit peuvent avoir des effets inattendus ailleurs dans le code. Il est difficile de garder une trace de toutes les variables qui pourraient se référer à un objet donné.

La copie d'un objet est souvent une alternative judicieuse à l'aliasing. Julia propose une fonction appelée deepcopy qui peut dupliquer tout objet :

julia> p1 = MPoint(3.0, 4.0) 
MPoint(3.0, 4.0) 
julia> p2 = deepcopy(p1) 
MPoint(3.0, 4.0) 
julia> p1 ≡ p2 
false 
julia> p1 == p2 
false

L'opérateur ≡ indique que p1 et p2 ne constituent pas le même objet, ce qui est attendu. En revanche, on aurait pu attendre que == donne true, car ces points contiennent les mêmes données. Dans ce cas, il faut être attentif au fait que, pour les objets non persistants, le comportement par défaut de l'opérateur == est le même que celui de l'opérateur ===. L'opérateur == vérifie l'identité de l'objet et non son équivalence. C'est parce que, pour les types composites non persistants, Julia ne sait pas ce qui doit être considéré comme équivalent (du moins, pas encore).

15-7-1. Exercice 15-2▲

Lorsqu'on commence à travailler avec des objets, de nouvelles exceptions sont susceptibles d'apparaître. Par exemple, une tentative d'accès à un champ qui n'existe pas se solde par une erreur :

julia> p = Point(3.0, 4.0) 
Point(3.0, 4.0)
julia> p.z = 1.0 
ERROR: type Point has no field z Stacktrace: [1] setproperty!(::Point, ::Symbol, ::Float64) at ./sysimg.jl:19 [2] top-level scope at none:0

Au cas où vous ne seriez pas sûr du type d'objet, il convient de le demander à Julia :

julia> typeof(p)
Point

La fonction isa est également utilisable pour vérifier qu'un objet est bel et bien une instance d'un type :

julia> p isa Point
true

S'il n'est pas sûr qu'un objet possède un attribut particulier, la fonction interne fieldnames s'avère utile :

julia> fieldnames(Point)
(:x, :y)

Alternativement, la fonction isdefined est utilisable :

julia> isdefined(p, :x)
true
julia> isdefined(p, :z)
false

Le premier argument désigne tout objet. Le deuxième argument est composé du symbole : suivi du nom du champ.

struct type composite.

constructeur fonction portant le même nom qu'un type qui crée des instances de ce type.

instance objet qui appartient à un type.

instancier créer un nouvel objet.

attribut ou champ une des valeurs nommées associées à un objet.

objet intégré objet « enchassé » dans le champ d'un autre objet.

duplication (deep copy) action de copier le contenu d'un objet, ainsi que tous les objets qui y sont intégrés et ainsi de suite. La duplication est mise en œuvre par la fonction deepcopy.

diagramme d'objet diagramme qui montre les objets, leurs champs et les valeurs des champs.

15-10-1. Exercice 15-3▲

15-10-2. Exercice 15-4▲