Think Julia

Un programme est une séquence d'instructions qui établit la manière d'effectuer un calcul. Le calcul peut être mathématique, comme la résolution d'un système d'équations ou la recherche des racines d'un polynôme, mais il peut aussi être symbolique, comme la recherche et le remplacement de texte dans un document, ou encore graphique, comme le traitement d'une image ou la lecture d'une vidéo.

Les détails sont différents selon les langages, mais quelques instructions élémentaires apparaissent dans presque chaque langage :

Données en entrée : il s'agit d'incorporer des données en provenance du clavier, d'un fichier, du réseau ou d'un autre appareil ;

Sortie : il s'agit d'afficher les données à l'écran, les enregistrer dans un fichier, les envoyer sur le réseau, etc. ;

Mathématiques : il s'agit d'effectuer des opérations mathématiques de base comme l'addition, la multiplication, etc. ;

Exécution conditionnelle : il s'agit de vérifier certaines conditions et, en conséquence, de lancer le code approprié ;

Répétition : il s'agit d'effectuer une action de manière répétée, généralement avec une variation donnée.

C'est à peu près tout. Chaque programme que nous avons utilisé, aussi complexe soit-il, est composé d'instructions qui ressemblent à ce qui est décrit précédemment. Nous considérerons donc la programmation comme le processus de décomposition d'une tâche ample et complexe en sous-tâches de plus en plus petites, jusqu'à ce que les sous-tâches soient suffisamment simples pour être exécutées à l'aide de ces instructions de base.

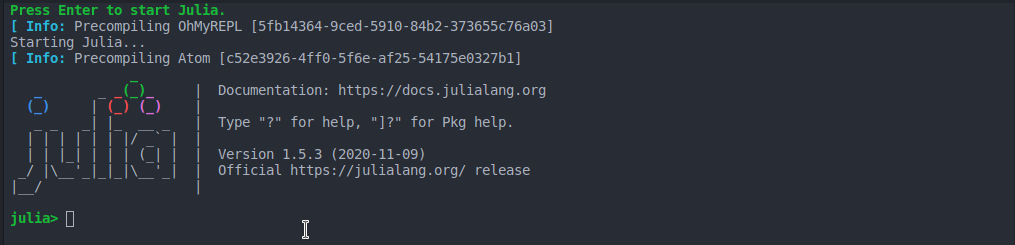
Après avoir lancé Visual Studio Codium (voir l'annexe BAnnexe B : Installation de Julia), nous arrivons sur une page telle que celle de la figure 1.2.1.

Le REPL (Read-Eval-Print Loop) de Julia est un programme qui lit et exécute le code Julia. Le REPL est exécutable en ouvrant un terminal sur JuliaBox et en saisissant julia sur la ligne de commande. Quand le REPL démarre, nous devrions voir l'information telle que reprise dans la figure 1.2.1.

Les premières lignes contiennent des informations sur le REPL, il se peut donc que ce soit un peu différent. Il faut vérifier que le numéro de version est au moins 1.0.0.

La dernière ligne est une invite qui indique que le REPL est prêt pour que nous puissions saisir du code.

Si nous saisissons une ligne de code et appuyons sur ENTER, le REPL affiche le résultat :

julia> 1 + 1
2

Traditionnellement, le premier programme à écrire dans un nouveau langage informatique s'appelle « Hello, World! », bien qu'il n'affiche que l'expression Hello, World!. Avec Julia, le code se présente comme ceci :

julia> println("Hello, World!")
Hello, World!

Il s'agit d'un exemple d'instruction permettant un affichage (à l'écran) avec retour à la ligne. Les guillemets droits marquent le début et la fin du texte à afficher ; ils n'apparaissent pas dans le résultat. Les parenthèses indiquent que println est une fonction (voir le chapitre 3Fonctions).

L'étape suivante concerne l'arithmétique. Julia fournit des opérateurs de multiplication, de division, d'addition et de soustraction. Les opérateurs +, - et * effectuent des additions, des soustractions et des multiplications, comme dans les exemples suivants :

julia> 40 + 2
42
julia> 43 - 1
42
julia> 6 * 7
42

L'opérateur / effectue la division :

julia> 84 / 2
42.0

Pourquoi le résultat est-il 42.0 au lieu de 42 ? Ceci est expliqué dans la section 1.5Valeurs et types. Enfin, l'opérateur ^ élève un nombre à une puissance donnée :

julia> 6^2 + 6
42

Une valeur est un des éléments de base avec lesquels un programme fonctionne, comme une lettre ou un nombre. Certaines des valeurs que nous avons vues jusqu'ici sont 2, 42.0 et "Hello, World!".

Ces valeurs appartiennent à différents types : 2 est un nombre entier, 42.0 un nombre à virgule flottante et "Hello, World!" une chaîne de caractères.

S'il y a un doute sur le type d'une valeur, le REPL peut fournir des renseignements :

julia> typeof(2)
Int64
julia> typeof(42.0)
Float64
julia> typeof("Hello, World!")
String

Les nombres entiers appartiennent au type Int64, les chaînes de caractères au type String et les nombres à virgule flottante au type Float64.

Qu'en est-il des valeurs comme "2" et "42.0" ? Elles ressemblent à des nombres, mais comme elles sont entre guillemets, il s'agit de chaînes de caractères :

julia> typeof("2")
String
julia> typeof("42.0")
String

Lorsque des nombres constitués de nombreux chiffres sont saisis, il peut être tentant d'utiliser des virgules entre les groupes de chiffres, comme pour exprimer un million en notation anglo-saxonne : 1,000,000. Ceci n'est pas un nombre entier autorisé en langage Julia, bien que cette représentation soit licite :

julia> 1,000,000
(1, 0, 0)

Évidemment, ce n'est pas du tout le résultat espéré. Julia analyse 1,000,000 comme une suite d'entiers, à savoir 1, 0 et 0, séparés par des virgules. Ce type de séquences sera analysé plus tard. Il est cependant possible d'obtenir le résultat recherché en utilisant 1_000_000.

Les langages naturels sont ceux que les êtres humains utilisent quotidiennement, comme l'anglais, l'espagnol, le français, etc. Ils n'ont pas été conçus d'un bloc par leurs utilisateurs parce qu'ils ont évolué naturellement et progressivement.

A contrario, les langages formels sont conçus pour des applications spécifiques. Par exemple, la notation utilisée par les mathématiciens est un langage formel particulièrement efficace pour établir les relations entre les nombres et les symboles. Les chimistes utilisent un langage formel pour représenter la structure chimique des molécules et les réactions. Les langages de programmation sont des langages formels qui ont été conçus pour effectuer des calculs.

Le cœur des langages formels est constitué de règles syntaxiques strictes qui organisent la structure des énoncés. Par exemple, en mathématiques, l'énoncé 3+3=6 a une syntaxe correcte, mais 3+=3$6 n'a pas de sens. En chimie, H₂O est une formule syntaxiquement correcte, cependant que ₂Zz ne l'est pas.

Les règles syntaxiques se déclinent en deux types, relatives aux signes d'une part et à la structure, de l'autre. Les signes sont les éléments de base de tout langage, tels que les mots, les nombres et les éléments chimiques. Un des problèmes avec 3+=3$6 est que $ n'est en principe pas un signe autorisé en mathématiques. De même, ₂Zz n'est pas licite, car il n'y a pas d'élément de symbole Zz. Le deuxième type de règle syntaxique concerne la manière dont les signes sont combinés. L'équation 3+=3 est incorrecte, car, même si + et = sont des signes autorisés, leur succession n'est pas définie en mathématiques et n'a dès lors pas de sens. De même, dans une formule chimique, l'indice vient éventuellement après le nom d'un élément, jamais avant.

Voici un exemple curieux : l@ phrase de françai$ bien structurée avec des s*gnes mal utilisés. Tous les signes de cette phrase sont valides, mais la structure de la phrase est erronée.

La lecture d'une phrase en français ou une déclaration dans une langue formelle suppose d'en comprendre la structure (bien que, dans une langue naturelle, tout lecteur procède ainsi, inconsciemment). Ce processus s'appelle l'analyse syntaxique. Bien que les langues formelles et naturelles aient de nombreuses caractéristiques en commun — les signes, la structure et la syntaxe —, il existe quelques différences notoires :

Ambiguïté : les langues naturelles sont chargées d'ambiguïté, que les humains gèrent en utilisant des indices contextuels ainsi que d'autres informations. Les langues formelles sont conçues pour être presque ou totalement dépourvues d'ambiguïté, ce qui signifie que toute déclaration a une — et une seule — signification, quel que soit le contexte ;

Redondance : pour pallier l'ambiguïté et réduire les malentendus, les langues naturelles sont caractérisées par de nombreuses redondances. De ce fait, elles sont souvent verbeuses. Les langues formelles sont moins redondantes et plus concises ;

Littéralité : les langues naturelles sont remplies d'expressions idiomatiques et de métaphores. Dans l'expression « le franc est tombé », il y a fort à parier qu'il n'y a pas de franc en jeu et que rien ne tombe (cette expression idiomatique signifie que quelqu'un a compris quelque chose après une période de confusion). Les langues formelles signifient exactement ce qu'elles disent. Comme nous grandissons tous en parlant des langues naturelles, il est parfois difficile de s'adapter aux langues formelles. La différence entre le langage formel et le langage naturel s'apparente à la différence entre la poésie et la prose, mais en plus :

• Poésie : les mots sont utilisés pour leurs sons ainsi que pour leur signification. L'ensemble du poème crée un effet ou une réponse émotionnelle. L'ambiguïté est non seulement courante, mais souvent délibérée,
• Prose : le sens littéral des mots est important et la structure apporte du sens. La prose se prête davantage à l'analyse que la poésie, mais reste néanmoins souvent ambiguë ;

Programmes : la signification d'un programme informatique est sans ambiguïté et littérale, elle peut être entièrement comprise par l'analyse des signes et de la structure.

Les langages formels sont plus denses que les langues naturelles, ce qui nécessite plus de temps et de concentration pour les interpréter. De plus, la structure est fondamentale. Il n’est donc pas toujours judicieux de lire de haut en bas et de gauche à droite. Au lieu de cela, le lecteur apprend à analyser le programme mentalement, à identifier les signes et à interpréter la structure. Enfin, les détails sont importants. De petites erreurs d'orthographe ou de ponctuation, dont il est possible de s'affranchir dans les langues naturelles, peuvent entraîner des incompréhensions dans un langage formel.

Tous les programmeurs commettent des erreurs. Pour des raisons quelque peu fantaisistes, les erreurs de programmation sont appelées « bogues » et le processus pour les débusquer est appelé « débogage » (debugging). La programmation, et surtout le débogage, font parfois surgir des émotions fortes. Confronté à un bogue difficile, un programmateur peu aguerri peut se sentir en colère, découragé ou frustré. Il est prouvé que de très nombreuses personnes réagissent naturellement face aux ordinateurs comme si ces derniers étaient des personnes. Lorsque les ordinateurs fonctionnent bien, nous les considérons comme des coéquipiers, mais, lorsqu'ils se montrent obstinés, nous leur répondons de la même manière que si nous répondions à des personnes obstinées.

Se préparer à ces réactions aide à les surmonter. Une approche possible consiste à considérer l'ordinateur comme un employé doté de certains atouts tels la rapidité et la précision, mais aussi de faiblesses particulières, comme le manque d'empathie et l'incapacité à saisir la situation dans son ensemble. Le travail d'un programmeur consiste à être un bon gestionnaire : trouver des moyens de tirer parti des points forts et d'atténuer les points faibles, trouver des moyens d'effacer ses émotions pour s'attaquer au problème, sans laisser ses réactions interférer avec sa capacité à travailler efficacement.

Apprendre à déboguer peut être frustrant, mais un bon débogueur possède une compétence précieuse très utile pour de nombreuses activités au-delà même de la programmation. À la fin de chaque chapitre, existe une section comme celle-ci, comportant diverses suggestions supposées utiles pour le débogage.

résolution des problèmes : processus consistant à formuler un problème, à trouver une solution et à l'exprimer.

programme : séquence d'instructions qui explicite un calcul.

REPL : programme qui lit les données d'entrée, les exécute et produit des résultats de manière répétée.

invite : caractères affichés par le REPL pour indiquer qu'il est prêt à recevoir les données de l'utilisateur.

déclaration : instruction qui amène le REPL à afficher une valeur à l'écran.

opérateur : symbole qui permet l'exécution d'un calcul simple comme l'addition, la multiplication de nombres ou la concaténation de chaînes de caractères.

valeur : une des unités de base des données, comme un nombre ou une chaîne de caractères, qu'un programme manipule.

type : une catégorie de valeurs. Les types vus jusqu'à présent sont les nombres entiers (Int64), les nombres à virgule flottante (Float64) et les chaînes de caractères (String).

Int : type qui représente des nombres entiers.

Float : type qui représente les nombres avec un point décimal.

Char : type qui représente des caractères uniques.

langage naturel : toute langue que parlent les Hommes et qui a évolué naturellement.

langage formel : tout langage que les humains ont conçu à des fins spécifiques, comme la représentation de principes mathématiques ou de programmes informatiques. Tous les langages de programmation sont des langages formels.

syntaxe : règles qui organisent la structure d'un programme.

signe : élément de base de la structure syntaxique d'un programme, analogue à un mot dans une langue naturelle.

structure : façon dont les signes sont combinés.

parse (analyse) : examen d'un programme et analyse de la structure syntaxique.

bug (ou bogue) : erreur dans un programme.

débogage : processus de recherche et de correction des bogues.

1-9-1. Exercice 1-1▲

1-9-2. Exercice 1-2▲